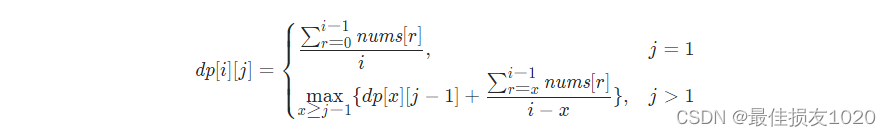leetcode记录

推荐博客
五大常用算法：分治、动态规划、贪心、回溯和分支界定
==刷题时注意边界条件/特殊条件的处理==

代码复制粘贴太多了，编辑起来很卡，再开一个博客：leetcode记录2

合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

思路：简单的合并链表，刚开始的思路是每次循环找到最小的节点，后面看题解发现可以使用优先队列这种方式辅助找到最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
 public:
  bool IterToEnd(vector<ListNode*>& lists) {  // 所有链表均遍历至尾部
    for (auto& link_list : lists) {
      if (link_list != nullptr) {
        return false;
      }
    }
    return true;
  }

  ListNode* mergeKLists(vector<ListNode*>& lists) {
    ListNode virt_node;
    ListNode* p = &virt_node;
    while (!IterToEnd(lists)) {
      // 找到最小的链表节点与下标
      int min_val = 1UL << 30;
      int min_index = -1;
      for (int i = 0; i < lists.size(); i++) {
        if (lists[i] != nullptr) {
          if (min_val > lists[i]->val) {
            min_val = lists[i]->val;
            min_index = i;
          }
        }
      }
      // 将该节点加入合并链表
      p->next = lists[min_index];
      p = lists[min_index];
      lists[min_index] = lists[min_index]->next;
    }
    return virt_node.next;
  }
};

使用优先队列找到最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  ListNode* mergeKLists(vector<ListNode*>& lists) {
    ListNode virt_node;
    ListNode* p = &virt_node;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> node_queue;
    for (int i = 0; i < lists.size(); i++) {
      if (lists[i] != nullptr) {
        node_queue.emplace(lists[i]->val, i);  // 加入链表节点值与对应下标
      }
    }
    while (!node_queue.empty()) {
      auto [_, min_index] = node_queue.top();
      node_queue.pop();
      p->next = lists[min_index];
      p = lists[min_index];
      lists[min_index] = lists[min_index]->next;
      if (lists[min_index] != nullptr) {  // 加入其后的链表节点
        node_queue.emplace(lists[min_index]->val, min_index);
      }
    }
    return virt_node.next;
  }
};

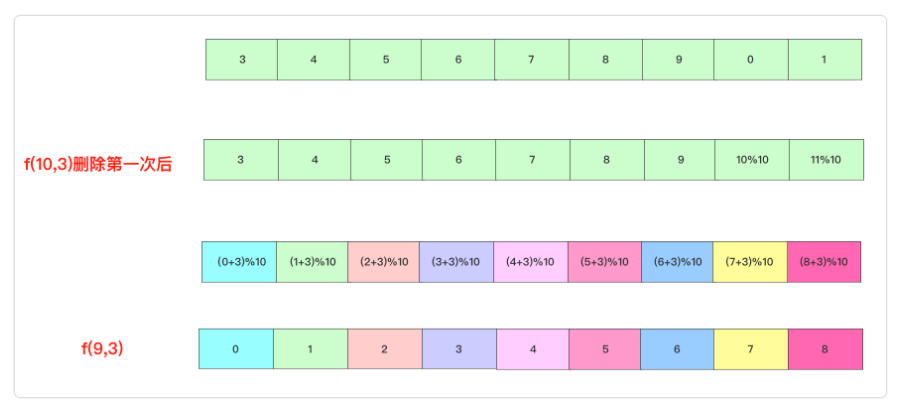
圆圈中最后剩下的数字

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

记住约瑟夫环的递推公式即可

1
2
3
4
5
6
7
8
9
10
11
class Solution {
 public:
  int lastRemaining(int n, int m) {
    // 递推公式 f(n,m) = (f(n-1,m)+m)%n;
    int value = 0;
    for (int i = 2; i <= n; i++) {
      value = (value + m) % i;
    }
    return value;
  }
};

字符串相加

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和并同样以字符串形式返回。

按我之前的写法，我的代码会像这样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
string add(string a, string b, int radix) {
  reverse(a.begin(), a.end());
  reverse(b.begin(), b.end());
  int len_a = a.length();
  int len_b = b.length();
  a += string((50 - len_a), '0');
  b += string((50 - len_b), '0');
  int flag = 0;
  for (int i = 0; i < 50; i++) {
    int sum = a[i] + b[i] - '0' - '0' + flag;
    flag = 0;
    if (sum >= radix) {
      sum = sum - radix;
      flag = 1;
    }
    a[i] = sum + '0';
  }
  int len = len_a > len_b ? len_a : len_b;
  while (a[len] != '0') {
    len++;
  }
  string ans = a.substr(0, len);
  reverse(ans.begin(), ans.end());
  return ans;
}

看了字符串相乘的代码后，我写出来这样的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
 public:
  string addStrings(string num1, string num2) {
    int len1 = num1.size();
    int len2 = num2.size();
    if (len1 < len2) {  // 保证len1>=len2
      swap(num1, num2);
      swap(len1, len2);  // 记得交换len
    }

    vector<int> ans(len1 + 1, 0);  // 多申请一位空间
    // 从右往左计算
    for (int i = 0; i < len2; i++) {
      ans[len1 - i] = num1[len1 - i - 1] + num2[len2 - i - 1] - 2 * '0';
    }
    for (int i = len2; i < len1; i++) {
      ans[len1 - i] = num1[len1 - i - 1] - '0';
    }
    
    for (int i = len1; i > 0; i--) {
      ans[i - 1] += ans[i] / 10;  // 进位
      ans[i] = ans[i] % 10;
    }
    int start = (ans[0] == 0) ? 1 : 0;
    string ans_str;
    for (int i = start; i <= len1; i++) {
      ans_str.push_back(ans[i] + '0');
    }
    return ans_str;
  }
};

而官方的题解仍然是最简洁的，一个循环解决问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
 public:
  string addStrings(string num1, string num2) {
    int i = num1.length() - 1;
    int j = num2.length() - 1;
    int carry = 0;
    string ans;
    while ((i >= 0) || (j >= 0) || (carry > 0)) {
      int x = (i >= 0) ? num1[i] - '0' : 0;
      int y = (j >= 0) ? num2[j] - '0' : 0;
      int sum = x + y + carry;
      ans.push_back(sum % 10 + '0');
      carry = sum / 10;
      i--;
      j--;
    }
    reverse(ans.begin(), ans.end());
    return ans;
  }
};

相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

直接借助set实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
 public:
  ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
    unordered_set<ListNode *> se;
    while (headA != nullptr) {
      se.emplace(headA);
      headA = headA->next;
    }
    while (headB != nullptr) {
      if (se.count(headB) > 0) {
        return headB;
      }
      headB = headB->next;
    }
    return nullptr;
  }
};

然后便是官方题解的巧妙解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
 public:
  ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
    if (headA == nullptr || headB == nullptr) {
      return nullptr;
    }
    ListNode *pA = headA;
    ListNode *pB = headB;
    while (pA != pB) {
      pA = (pA == nullptr) ? headB : pA->next;
      pB = (pB == nullptr) ? headA : pB->next;
    }
    return pA;
  }
};

环形链表与Floyd判圈算法

141.环形链表
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中存在环 ，则返回 true 。 否则，返回 false 。

142.环形链表 II
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
不允许修改 链表。

首先，使用最简单的思路，借助set实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
 public:
  bool hasCycle(ListNode* head) {
    ListNode* cur = head;
    set<ListNode*> se;
    while (cur != nullptr) {
      if (se.count(cur) > 0) {
        return true;
      }
      se.emplace(cur);
      cur = cur->next;
    }
    return false;
  }
};

class Solution {
 public:
  ListNode* detectCycle(ListNode* head) {
    ListNode* cur = head;
    unordered_set<ListNode*> se;
    while (cur != nullptr) {
      if (se.count(cur) > 0) {
        return cur;
      }
      se.emplace(cur);
      cur = cur->next;
    }
    return nullptr;
  }
};

利用Floyd算法，使用快慢指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
 public:
  bool hasCycle(ListNode* head) {
    if (head == nullptr || head->next == nullptr) {
      return false;
    }
    // 快慢指针
    ListNode* slow = head;
    ListNode* fast = head;
    do { // 使用do while，省去第一次判断
      if (fast == nullptr || fast->next == nullptr) {	// 到达末尾，不存在环
        return false;
      }
      slow = slow->next;		// 前进一步
      fast = fast->next->next;	// 前进两步
    } while (slow != fast);
    return true;
  }
};

class Solution {
 public:
  ListNode* detectCycle(ListNode* head) {
    if (head == nullptr || head->next == nullptr) {
      return false;
    }
    // 快慢指针
    ListNode* slow = head;
    ListNode* fast = head;
    do {
      if (fast == nullptr || fast->next == nullptr) {
        return nullptr;
      }
      slow = slow->next;
      fast = fast->next->next;
    } while (slow != fast);
    // 从起点与快慢指针相遇点出发，直到在入口点相遇
    ListNode* cur = head;
    while (cur != slow) {
      cur = cur->next;
      slow = slow->next;
    }
    return cur;
  }
};

反转链表 II

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

分类讨论，是否从最开始进行反转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
 public:
  ListNode* reverseBetween(ListNode* head, int left, int right) {
    if (head->next == nullptr) {  // 只有一个节点
      return head;
    }
    ListNode* left_node_prev;
    ListNode* left_node;
    if (left == 1) {  // 起始节点，则前置节点为空
      left_node_prev = nullptr;
      left_node = head;
    } else {
      left_node_prev = head;
      for (int i = 1; i < left - 1; i++) {
        left_node_prev = left_node_prev->next;
      }
      left_node = left_node_prev->next;
    }

    ListNode* prev = left_node;
    ListNode* curr = left_node->next;
    ListNode* next;
    for (int i = left; i < right; i++) {
      next = curr->next;
      curr->next = prev;
      prev = curr;
      curr = next;
    }
    // 此时curr next为right node后继节点，prev为right node
    left_node->next = curr;
    if (left_node_prev != nullptr) {  // 此时链表头部并未改变
      left_node_prev->next = prev;
      return head;
    }
    // 从头开始反转，头部改变
    return prev;
  }
};

使用虚拟头结点，合并两种情况，统一处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
 public:
  ListNode* reverseBetween(ListNode* head, int left, int right) {
    if (head->next == nullptr) {  // 只有一个节点
      return head;
    }
    ListNode virt_head(-1, head);  // 虚拟头节点，便于统一处理
    // 迭代至正确的左节点前置节点
    ListNode* left_node_prev = &virt_head;
    for (int i = 1; i < left; i++) {
      left_node_prev = left_node_prev->next;
    }
    ListNode* left_node = left_node_prev->next;
    ListNode* prev = left_node;
    ListNode* curr = left_node->next;  // 处理左节点后继节点
    ListNode* next;
    for (int i = left; i < right; i++) {
      next = curr->next;  // 保存后继节点
      curr->next = prev;  // 转向
      // 向前移动
      prev = curr;
      curr = next;
    }
    // 此时curr next为right node后继节点，prev为right node
    // 连接反转链表的头尾
    left_node->next = curr;
    left_node_prev->next = prev;
    return virt_head.next;
  }
};

搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

对题目有些误解，并不是一定旋转，将数组分为左半部右半部，若在不同分部，则一定向该方向前进，其他情况照常

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
 public:
  int search(vector<int>& nums, int target) {
    if (nums.size() == 1) {
      return nums[0] == target ? 0 : -1;
    }

    int left_min = nums[0];
    int right_max = nums[nums.size() - 1];
    if (right_max < left_min) {             // 进行旋转
      bool in_left = target >= left_min;    // 数字位于左半部
      bool in_right = target <= right_max;  // 数字位于右半部
      if (!in_left && !in_right) {
        return -1;
      }
      int high = nums.size() - 1;
      int low = 0;
      while (low <= high) {
        int mid = (low + high) / 2;
        if (nums[mid] == target) {  // 恰好相等，返回索引
          return mid;
        } else if (in_left && nums[mid] <= right_max) {  // 位置不一致，向左前进
          high = mid - 1;
        } else if (in_right && nums[mid] >= left_min) {  // 位置不一致，向右前进
          low = mid + 1;
        } else if (nums[mid] > target) {  // 位置一致，向左前进
          high = mid - 1;
        } else if (nums[mid] < target) {  // 位置一致，向右前进
          low = mid + 1;
        }
      }
    } else {  // 未进行旋转
      int high = nums.size() - 1;
      int low = 0;
      while (low <= high) {
        int mid = (low + high) / 2;
        if (nums[mid] == target) {  // 恰好相等，返回索引
          return mid;
        } else if (nums[mid] > target) {  // 位置一致，向左前进
          high = mid - 1;
        } else if (nums[mid] < target) {  // 位置一致，向右前进
          low = mid + 1;
        }
      }
    }

    return -1;
  }
};

使用官方题解的方法，将数组分为有序部分与无序部分，利用有序部分特性与排除法锁定target所在

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
 public:
  int search(vector<int>& nums, int target) {
    int low = 0;
    int high = nums.size() - 1;
    while (low < high) {
      int mid = (low + high) / 2;
      if (nums[mid] == target) {  // 找到目标值，返回下标
        return mid;
      }
      if (nums[low] <= nums[mid]) {                       // 前半部有序
        if (nums[low] <= target && target < nums[mid]) {  // target是否存在前半部
          high = mid - 1;
        } else {
          low = mid + 1;
        }
      } else {                                             // 后半部有序
        if (nums[mid] < target && target <= nums[high]) {  // target是否存在后半部
          low = mid + 1;
        } else {
          high = mid - 1;
        }
      }
    }

    return nums[low] == target ? low : -1;  // 判断最后一个元素是否为目标值
  }
};

格雷编码

n 位格雷码序列 是一个由 2n 个整数组成的序列，其中：
每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
第一个整数是 0
一个整数在序列中出现 不超过一次
每对 相邻 整数的二进制表示 恰好一位不同 ，且
第一个 和 最后一个 整数的二进制表示 恰好一位不同
给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
 public:
  vector<int> grayCode(int n) {
    vector<int> ans;
    ans.emplace_back(0);
    for (int i = 1; i <= n; i++) {
      for (int j = ans.size() - 1; j >= 0; j--) {  // 加入上半部的倒转，并将高位置一
        ans.emplace_back(ans[j] | (1 << (i - 1)));
      }
    }
    return ans;
  }
};

字符串相乘

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

我的解法是利用字符串相加+字符串乘整数实现字符串乘法，非常繁杂的算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
 public:
  void add(string& num1, const string& num2) {  // num1 = num1 + num2，保证num1[i]永不越界
    int carry = 0;
    int i;
    for (i = 0; i < num2.size(); i++) {
      int sum = num1[i] + num2[i] - 2 * '0' + carry;
      num1[i] = sum % 10 + '0';
      carry = sum / 10;
    }
    while (carry != 0) {
      int sum = num1[i] - '0' + carry;
      num1[i] = sum % 10 + '0';
      carry = sum / 10;
      i++;
    }
  }
  string simpleMulti(string num1, int x) {  // res = num1 * x,保证num1[i]永不越界，carry结束for循环后为0
    int carry = 0;
    for (int i = 0; i < num1.size(); i++) {
      int sum = (num1[i] - '0') * x + carry;
      num1[i] = sum % 10 + '0';
      carry = sum / 10;
    }
    return num1;
  }
  string multiply(string num1, string num2) {  // 没有前导零与后导零
    if (num1 == "0" || num2 == "0") {          // 排除结果为0的特殊情况
      return "0";
    }
    string ans(num1.size() + num2.size() + 3, '0');  // 申请足够大的空间，避免溢出
    reverse(num1.begin(), num1.end());               // 反转num1
    num1.push_back('0');                             // 加入一个前导零，简化乘法carry计算
    for (int i = 0; i < num2.size(); i++) {
      string local_multi = simpleMulti(num1, num2[i] - '0');  // num1 * x
      string prefix(num2.size() - 1 - i, '0');                // 加入若干位0，移位运算
      add(ans, prefix + local_multi);                         // ans += num1 * x * 10^y
    }

    int end = ans.length() - 1;  // 从后往前数第一个不为'0'的坐标
    while (ans[end] == '0') {
      end--;
    }
    reverse(ans.begin(), ans.begin() + end + 1);  // 反转，得到最终结果
    return ans.substr(0, end + 1);
  }
};

官方题解使用vector从右往左向乘，结果位数要么为m+n-1,m+n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
 public:
  string multiply(string num1, string num2) {
    if (num1 == "0" || num2 == "0") {
      return "0";
    }
    int len1 = num1.length();
    int len2 = num2.length();
    vector<int> ans_arr(len1 + len2);  // 用int存储每一位的数
    // 从右往前乘
    for (int i = len1 - 1; i >= 0; i--) {
      for (int j = len2 - 1; j >= 0; j--) {
        ans_arr[i + j + 1] += (num1[i] - '0') * (num2[j] - '0');
      }
    }
    for (int i = len1 + len2 - 1; i > 0; i--) {
      ans_arr[i - 1] += ans_arr[i] / 10;  // 向前进位
      ans_arr[i] %= 10;
    }
    int start = (ans_arr[0] == 0) ? 1 : 0;
    string ans;
    for (int i = start; i < len1 + len2; i++) {
      ans.push_back(ans_arr[i] + '0');
    }
    return ans;
  }
};

删除有序数组中的重复项

给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

我使用的方法是先遍历一遍，标记无效数字，然后再次遍历，将前面的无效数与后面的有效数交换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
const int kInvaild = 1 << 20;
class Solution {
 public:
  int removeDuplicates(vector<int>& nums) {
    int last_number = nums[0];
    int invaild_count = 0;
    for (int i = 1; i < nums.size(); i++) {
      if (nums[i] == last_number) {  // 重复数字
        nums[i] = kInvaild;
        invaild_count++;
      } else {
        last_number = nums[i];
      }
    }
    if (invaild_count == 0) {  // 数组没有重复数字
      return nums.size();
    }

    int new_len = nums.size() - invaild_count;
    int start = 0;
    int end = 0;
    while (start < new_len) {            // 数字迁移完成后start==new_len
      while (nums[start] != kInvaild) {  // 寻找第一个无效数（空位）
        start++;
      }
      if (start == new_len) {  // 边界条件
        break;
      }
      end = start;
      while (nums[end] == kInvaild) {  // 寻找第一个有效数
        end++;
      }
      swap(nums[start], nums[end]);  // 有效数无效数交换
      start++;
    }
    return new_len;
  }
};

而官方题解使用快慢指针的方法解决，非常简洁的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
 public:
  int removeDuplicates(vector<int>& nums) {
    // 快慢指针
    int fast = 1;
    int slow = 1;
    for (fast = 1; fast < nums.size(); fast++) {
      if (nums[fast] != nums[fast - 1]) {  // 不为重复数
        nums[slow] = nums[fast];
        slow++;
      }
    }
    return slow;
  }
};

字符串的排列

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

一：最简单的方法 dfs+set

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
 public:
  void dfs(set<string>& result, string& s, int start, int end) {  // 全排列+set去重
    if (start == end) {
      result.emplace(s);
      return;
    }
    for (int i = start; i < end; i++) {
      swap(s[i], s[start]);
      dfs(result, s, start + 1, end);
      swap(s[i], s[start]);
    }
  }
  vector<string> permutation(string s) {
    set<string> ans;
    dfs(ans, s, 0, s.length());
    return vector<string>(ans.begin(), ans.end());
  }
};

二： 有条件的dfs，我自己实现的代码只保证了没有与start重复，要保证该位置没有任何重复字符需利用set

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
 public:
  void dfs(vector<string>& result, string& s, int start, int end) {
    if (start == end) {
      result.emplace_back(s);
      return;
    }
    set<char> se;
    for (int i = start; i < end; i++) {
      // if (i != start && s[i] == s[start]) {  // 剪枝，只保证没有与s[start]重复
      //   continue;
      // }
      if (se.count(s[i]) != 0) {  // 保证该位置没有重复字符
        continue;
      }
      se.emplace(s[i]);
      swap(s[i], s[start]);
      dfs(result, s, start + 1, end);
      swap(s[i], s[start]);
    }
  }
  vector<string> permutation(string s) {
    vector<string> ans;
    dfs(ans, s, 0, s.length());
    return ans;
  }
};

三：巧妙利用下一个排列算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
 public:
  bool next(string& s) {  // 求字符串下一个排列，注意参数为引用传递
    int i;
    for (i = s.length() - 2; i >= 0; i--) {  // 寻找较小数
      if (s[i] < s[i + 1]) {
        break;
      }
    }
    if (i < 0) {
      return false;
    }
    for (int j = s.length() - 1; j >= 0; j--) {  // 寻找较大数
      if (s[j] > s[i]) {
        swap(s[i], s[j]);  // 交换
        break;
      }
    }
    reverse(s.begin() + i + 1, s.end());  // 反转
    return true;
  }
  vector<string> permutation(string s) {
    vector<string> ans;
    sort(s.begin(), s.end());  // 升序排列
    do {
      ans.emplace_back(s);
    } while (next(s));
    return ans;
  }
};

用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

简单题，但我的实现非常慢，因为我解决deleteHead的方法就是立即转移所有数据至另一个栈，没有想到部分数据迁移

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class CQueue {
 public:
  CQueue() : in_normal_{true} {}

  void appendTail(int value) {
    if (!in_normal_) {  // 当前在反转栈，需转移数据
      while (!reverse_.empty()) {
        normal_.emplace(reverse_.top());
        reverse_.pop();
      }
      in_normal_ = true;
    }
    normal_.emplace(value);
  }

  int deleteHead() {
    if (in_normal_) {  // 当前在正常栈，需转移数据
      while (!normal_.empty()) {
        reverse_.emplace(normal_.top());
        normal_.pop();
      }
      in_normal_ = false;
    }
    if (reverse_.empty()) {
      return -1;
    }
    int ans = reverse_.top();
    reverse_.pop();
    return ans;
  }

 private:
  stack<int> normal_;   // 在正常的栈
  stack<int> reverse_;  // 在反转的栈
  bool in_normal_;      // 记录数据位置
};

官方题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class CQueue {
 public:
  CQueue() {}

  void appendTail(int value) { in_stack_.emplace(value); }

  int deleteHead() {
    if (out_stack_.empty()) {  // 若输出栈为空则转移元素
      if (in_stack_.empty()) {
        return -1;
      }
      while (!in_stack_.empty()) {
        out_stack_.emplace(in_stack_.top());
        in_stack_.pop();
      }
    }
    int ans = out_stack_.top();  // 输出栈栈顶元素
    out_stack_.pop();
    return ans;
  }

 private:
  stack<int> in_stack_;   // 输入栈
  stack<int> out_stack_;  // 输出栈
};

不同的二叉搜索树 II

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

刚开始的时候我一直返回{}，而不是{nullptr}，有时候将空指针视作一个节点便于理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
 public:
  vector<TreeNode *> generate(int start, int end) {
    if (start > end) {
      return {nullptr};  // 关键点，没放入空指针
    }
    if (start == end) {
      return {new TreeNode(start)};
    }
    vector<TreeNode *> ans;
    for (int i = start; i <= end; i++) {
      auto left = generate(start, i - 1);
      auto right = generate(i + 1, end);
      for (auto left_node : left) {
        for (auto right_node : right) {
          TreeNode *root = new TreeNode(i);
          root->left = left_node;
          root->right = right_node;
          ans.emplace_back(root);
        }
      }
    }
    return ans;
  }
  vector<TreeNode *> generateTrees(int n) { return generate(1, n); }
};

和至少为 K 的最短子数组

给你一个整数数组 nums 和一个整数 k ，找出 nums 中和至少为 k 的 最短非空子数组 ，并返回该子数组的长度。如果不存在这样的 子数组 ，返回 -1 。

子数组 是数组中 连续 的一部分。

我的方法是简单的dp+枚举，但一直超出时间限制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
 public:
  int shortestSubarray(vector<int> &nums, int k) {
    vector<int> dp(nums.size());  // 以nums[i]结尾的最大连续和
    dp[0] = nums[0];
    for (int i = 1; i < nums.size(); i++) {
      dp[i] = nums[i] + max(0, dp[i - 1]);  // 要么加上之前的连续和，要么重新开始
    }
    int min_len = nums.size() + 1;
    for (int i = 0; i < nums.size(); i++) {
      if (nums[i] < 0) {  // 肯定不是最短子数组
        continue;
      }
      if (dp[i] >= k) {
        int sum = 0;
        int j = i;
        while (sum < k) {  // 向前累加，直至总和大于k
          sum += nums[j];
          j--;
        }
        min_len = min(min_len, i - j);  // 子数组长度
      }
    };
    return min_len <= nums.size() ? min_len : -1;
  }
};

而官方题解采用的是前缀和加双端递增序列的方式
两张图秒懂单调队列（Python/Java/C++/Go）

由于优化二保证了数据结构中的 s[i] 会形成一个递增的序列，因此优化一移除的是序列最左侧的若干元素，优化二移除的是序列最右侧的若干元素。我们需要一个数据结构，它支持移除最左端的元素和最右端的元素，以及在最右端添加元素，故选用双端队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  int shortestSubarray(vector<int> &nums, int k) {
    vector<long long> prefix(nums.size() + 1);  // p[i]-p[i-1] = s[0..i-1]
    prefix[0] = 0;
    for (int i = 1; i <= nums.size(); i++) {
      prefix[i] = prefix[i - 1] + nums[i - 1];
    }
    int min_len = nums.size() + 1;
    deque<int> q;  // 单调递增序列
    q.emplace_front(0);
    for (int i = 1; i <= nums.size(); i++) {
      while (!q.empty() && (prefix[i] - prefix[q.front()] >= k)) {  // 从左往右，寻找差值大于等于k的区间
        min_len = min(min_len, i - q.front());
        q.pop_front();
      }
      while (!q.empty() && prefix[i] <= prefix[q.back()]) {  // 维持单调递增关系
        q.pop_back();
      }
      q.emplace_back(i);
    }
    return min_len <= nums.size() ? min_len : -1;
  }
};

下一个更大元素 III

给你一个正整数 n ，请你找出符合条件的最小整数，其由重新排列 n 中存在的每位数字组成，并且其值大于 n 。如果不存在这样的正整数，则返回 -1 。

注意 ，返回的整数应当是一个 32 位整数 ，如果存在满足题意的答案，但不是 32 位整数 ，同样返回 -1 。

下一个排列算法的应用
一：借助vector拆解数字n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
 public:
  int nextGreaterElement(int n) {
    if (n < 10) {  // 个位数，提前退出
      return -1;
    }
    // 将每个位的数字压入数组
    vector<int> nums;
    while (n != 0) {
      nums.emplace_back(n % 10);
      n /= 10;
    }
    reverse(nums.begin(), nums.end());
    // 寻找较小数
    int i = 0;
    for (i = nums.size() - 2; i >= 0; i--) {
      if (nums[i] < nums[i + 1]) {
        break;
      }
    }
    if (i < 0) {  // 降序排列，最大值
      return -1;
    }
    // 寻找较大数并交换
    for (int j = nums.size() - 1; j >= 0; j--) {
      if (nums[j] > nums[i]) {
        swap(nums[i], nums[j]);
        break;
      }
    }
    // 对其后的数进行反转
    reverse(nums.begin() + i + 1, nums.end());
    long long ans = 0;
    for (int num : nums) {
      ans = ans * 10 + num;
    }
    return ans > INT_MAX ? -1 : ans;
  }
};

二：借助string拆解数字n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
 public:
  int nextGreaterElement(int n) {
    if (n < 10) {  // 个位数，提前退出
      return -1;
    }
    auto nums = to_string(n);
    // 寻找较小数
    int i = 0;
    for (i = nums.size() - 2; i >= 0; i--) {
      if (nums[i] < nums[i + 1]) {
        break;
      }
    }
    if (i < 0) {  // 降序排列，最大值
      return -1;
    }
    // 寻找较大数并交换
    for (int j = nums.size() - 1; j >= 0; j--) {
      if (nums[j] > nums[i]) {
        swap(nums[i], nums[j]);
        break;
      }
    }
    // 对其后的数进行反转
    reverse(nums.begin() + i + 1, nums.end());
    long long ans = stol(nums);
    return ans > INT_MAX ? -1 : ans;
  }
};

下一个排列

整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ，找出 nums 的下一个排列。

必须 原地 修改，只允许使用额外常数空间。
相关算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
 public:
  void nextPermutation(vector<int>& nums) {
    int i = 0, j = 0;
    for (i = nums.size() - 2; i >= 0; i--) {  // 找到第一个s[i]<s[i+1] 较小数
      if (nums[i] < nums[i + 1]) {
        break;
      }
    }
    if (i >= 0) {
      for (j = nums.size() - 1; j > i; j--) {  // 若找到i，则从后往前找到第一个比它大的数s[j] 较大数
        if (nums[j] > nums[i]) {
          break;
        }
      }
      swap(nums[i], nums[j]);  // 交换两数
    }
    reverse(nums.begin() + i + 1, nums.end());  // 一：若找到i，则将i后所有数反转 二：若未找到i，直接整体降序变升序
  }
};

分割回文串 II

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文。

返回符合要求的 最少分割次数 。

同样是之前没写出来的题目，同样现在也没想出来，动态规划总是看之前啥也想不出来，看之后恍然大悟，代码几行写完。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
 public:
  int minCut(string s) {
    int n = s.length();
    vector<vector<bool>> g(n, vector<bool>(n, true));  // g[i][j]表示s[i...j]是否为字符串
    for (int i = n - 2; i >= 0; i--) {
      for (int j = i + 1; j < n; j++) {
        g[i][j] = g[i + 1][j - 1] && (s[i] == s[j]);
      }
    }
    vector<int> f(n, n);  // f[i]为s[0...i]的最少分割次数
    for (int i = 0; i < n; i++) {
      if (g[0][i]) {  // 本身即为回文串，不用分割
        f[i] = 0;
      } else {
        for (int j = 0; j < i; j++) {
          if (g[j + 1][i]) {  // s[j+1...i]为回文字符串
            f[i] = min(f[i], f[j] + 1);
          }
        }
      }
    }
    return f[n - 1];
  }
};

我发现动态规划的解要不然就是聚合所有子问题的解（f[0…i-1]），要么就是聚合满足特定条件子问题的解（s[j+1…i]为回文字符串，f[i] = min(f[i], f[j] + 1)）

两数相除

给你两个整数，被除数 dividend 和除数 divisor。将两数相除，要求 不使用 乘法、除法和取余运算。

整数除法应该向零截断，也就是截去（truncate）其小数部分。例如，8.345 将被截断为 8 ，-2.7335 将被截断至 -2 。

返回被除数 dividend 除以除数 divisor 得到的 商 。

注意：假设我们的环境只能存储 32 位 有符号整数，其数值范围是 [−231, 231 − 1] 。本题中，如果商 严格大于 231 − 1 ，则返回 231 − 1 ；如果商 严格小于 -231 ，则返回 -231 。

同样是2019年没写出来的题目，现在同样也没写出来。官方题解使用快速乘+二分查找解决

当时我一直想的是将负数映射到正数有可能会溢出，分类讨论又太麻烦，却忘了可以将正数映射到负数，函数实现时最好首先把特殊情况排除，然后再实现通用功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
 public:
  bool check(int x, int y, int z) {  // z * y >= x 是否成立
    int cum = 0;                     // 奇数y乘积累加值
    int add = y;                     // y的乘积
    while (z) {
      if (z & 1) {
        // 需要保证 result + add >= x
        if (cum < x - add) {
          return false;
        }
        cum += add;
      }
      if (z != 1) {
        // 需要保证 add + add >= x
        if (add < x - add) {
          return false;
        }
        add += add;
      }
      // 不能使用除法
      z >>= 1;
    }
    return true;
  }
  int divide(int dividend, int divisor) {
    // 排除一系列的特殊情况
    if (dividend == INT_MIN && divisor == 1) {
      return INT_MIN;
    }
    if (dividend == INT_MIN && divisor == -1) {
      return INT_MAX;
    }
    if (divisor == INT_MIN) {
      return dividend == INT_MIN ? 1 : 0;
    }
    if (dividend == 0) {
      return 0;
    }
    // 全部变成负数
    bool rev = false;  // 结果是否乘以-1
    if (dividend > 0) {
      dividend = -dividend;
      rev = !rev;
    }
    if (divisor > 0) {
      divisor = -divisor;
      rev = !rev;
    }
    // 二分查找
    int left = 1;
    int right = INT_MAX;
    int ans = 0;
    while (left <= right) {
      int mid = left + ((right - left) >> 1);
      bool ret = check(dividend, divisor, mid);  // mid(+) * divisor(-) >= dividend(-)
      if (ret) {
        ans = mid;
        if (mid == INT_MAX) {
          break;
        }
        left = mid + 1;  // 左边界增大
      } else {
        right = mid - 1;  // 右边界减小
      }
    }
    return rev ? -ans : ans;
  }
};

K 站中转内最便宜的航班

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。 如果不存在这样的路线，则输出 -1。

这个题我2019年一直没做出来，我隐隐约约觉得是用BFS什么的做的，可我写了半天，越写越复杂，我就知道这一次我又做不出来了。看了看题解，动态规划，几行代码搞定，蚌！

当代码越来越复杂的时候，就可以想想是不是思路不正确了，而且这个时候大概率要用动态规划了。当题目中这种最多经过K个这种条件出现时，如果很容易放入最短路径的放缩条件，则照常使用最短路径算法，否则将其依次拆分为恰好为[0-k]时到达dst的路径长度，最终结果取其最值，很多的状态转移方程都是这种拆分+最值的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
 public:
  const int kMaxLen = (1 << 30);
  int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
    // 使用滚动数组存储f  f[t][j] 表示通过恰好t次航班，从出发城市src到达城市j需要的最小花费
    vector<vector<int>> f(2, vector<int>(n, kMaxLen));
    int pre = 0;
    int cur = 1;
    f[0][src] = 0;
    f[1][src] = 1;
    int ans = kMaxLen;
    for (int t = 1; t <= k + 1; t++) {
      for (auto& flight : flights) { // (i,j,cost)
        f[cur][flight[1]] = min(f[cur][flight[1]], f[pre][flight[0]] + flight[2]); // f[t][j] = min(f[t][j] , f[t−1][i]+cost(i,j))
      }
      ans = min(ans, f[cur][dst]);
      pre = (pre + 1) % 2;
      cur = (cur + 1) % 2;
    }
    return ans == kMaxLen ? -1 : ans;
  }
};

定义无穷值时最好不要定义为INT_MAX，这样就无法进行相加操作

N 字形变换

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 “PAYPALISHIRING” 行数为 3 时，排列如下：

1
2
3
P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：”PAHNAPLSIIGYIR”。

我的解法就是简单的分成两端，向下的序列和向上的序列，而后用两个for循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
 public:
  string convert(string s, int numRows) {
    int index = 0;
    vector<string> zigstr(numRows, "");
    while (index < s.length()) {
      for (int i = 0; i < numRows && index < s.length(); i++) {  // 向下
        zigstr[i].push_back(s[index]);
        index++;
      }
      for (int i = numRows - 2; i > 0 && index < s.length(); i--) {  // 向上
        zigstr[i].push_back(s[index]);
        index++;
      }
    }
    string ans = "";
    for (string& str : zigstr) {
      ans.append(str);
    }
    return ans;
  }
};

官方则简洁一点，将两个for循环合并在一起，且以index为下标递增，注意numRows = 1的特殊情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  string convert(string s, int numRows) {
    if (numRows == 1 || numRows >= s.length()) {  // 特殊情况，保证period大于0
      return s;
    }
    vector<string> zigstr(numRows, "");
    int row = 0;
    int period = 2 * numRows - 2;
    for (int i = 0; i < s.length(); i++) {
      zigstr[row].push_back(s[i]);
      if (i % period < numRows - 1) {
        row++;
      } else {
        row--;
      }
    }
    string ans = "";
    for (string& str : zigstr) {
      ans.append(str);
    }
    return ans;
  }
};

无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

刚开始我想的方法也是官方题解一样的使用set然后加入删除，但觉得这有点费劲，而且是字符，最大才255，就使用数组来存储，并分别记录每个位置的前一个相同字符位置和后一个相同字符，这样就能快速移动左右指针。右指针移动失败一定因为遇到相同字符或字符串末尾，而左指针可以直接跳转至该失败位置的前一个相同字符位置后+1，因为在其前面的位置都会在右指针位置失败，而长度均小于该次长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
 public:
  int lengthOfLongestSubstring(string s) {
    vector<int> last_occur_index(256, -1);                // 该字符上次出现的索引
    vector<int> next_same_index(s.length(), s.length());  // 下一个相同字符索引
    vector<int> pre_same_index(s.length(), s.length());   // 上一个相同字符索引
    for (int i = 0; i < s.length(); i++) {
      if (last_occur_index[s[i]] != -1) {
        next_same_index[last_occur_index[s[i]]] = i;
      }
      pre_same_index[i] = last_occur_index[s[i]];
      last_occur_index[s[i]] = i;
    }
    int start = 0;
    int max_substr_len = 0;
    while (start < s.length()) {
      int possible_bound = s.length();
      int end = start;
      while (end < possible_bound) {                                 // 小于可能的边界（下一个相同字符/字符串长度）
        possible_bound = min(possible_bound, next_same_index[end]);  // 下一个重复字符位置
        end++;
      }
      max_substr_len = max(max_substr_len, end - start);
      if (end >= s.length()) {
        return max_substr_len;
      }
      // 直接移动至失败位置的前一个相同字符位置后，在其前面的位置都会在end处失败
      start = pre_same_index[end] + 1;
    }
    return max_substr_len;
  }
};

最接近的三数之和

给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

我的思路比较简单，把一个数固定，解决最接近的两数之和，但在枚举时我采用的方法是将固定数置为无效，两数之和函数中还需对无效坐标进行特殊处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
 public:
  int twoSumClosest(const vector<int>& nums, int invaild_index, int target) {  // 求两数之和最接近target，invaild_index为无效下标
    int i = 0;
    int j = nums.size() - 1;
    int closest_sum = 0;
    int min_abs = INT32_MAX;
    while (i < j) {
      if (i == invaild_index) {
        i++;
      } else if (j == invaild_index) {
        j--;
      }
      if (i >= j) {  // 此时有可能违反条件
        return closest_sum;
      }
      
      int sum = nums[i] + nums[j];
      int abs_val = abs(sum - target);
      if (abs_val < min_abs) {
        min_abs = abs_val;
        closest_sum = sum;
      }

      if (sum > target) {
        j--;
      } else if (sum < target) {
        i++;
      } else {
        return target;
      }
    }
    return closest_sum;
  }

  int threeSumClosest(vector<int>& nums, int target) {
    sort(nums.begin(), nums.end());
    int three_closest_sum = 0;
    int min_abs = INT32_MAX;
    for (int i = 0; i < nums.size(); i++) {
      int two_closest_sum = twoSumClosest(nums, i, target - nums[i]);
      int abs_val = abs(two_closest_sum + nums[i] - target);
      if (abs_val < min_abs) {
        min_abs = abs_val;
        three_closest_sum = two_closest_sum + nums[i];
      }
    }
    return three_closest_sum;
  }
};

而官方题解比我的代码改进的点就在于每次只需枚举固定数后面的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
 public:
  int twoSumClosest(const vector<int>& nums, int start_index, int target) {  // 求两数之和最接近target，start_index为起始下标
    int i = start_index;
    int j = nums.size() - 1;
    int closest_sum = 0;
    int min_abs = INT32_MAX;
    while (i < j) {
      int sum = nums[i] + nums[j];
      int abs_val = abs(sum - target);
      if (abs_val < min_abs) {
        min_abs = abs_val;
        closest_sum = sum;
      }

      if (sum > target) {
        j--;
      } else if (sum < target) {
        i++;
      } else {
        return target;
      }
    }
    return closest_sum;
  }

  int threeSumClosest(vector<int>& nums, int target) {
    sort(nums.begin(), nums.end());
    int three_closest_sum = 0;
    int min_abs = INT32_MAX;
    for (int i = 0; i < nums.size() - 2; i++) {
      int two_closest_sum = twoSumClosest(nums, i + 1, target - nums[i]);  // [i+1,n-1]
      int abs_val = abs(two_closest_sum + nums[i] - target);
      if (abs_val < min_abs) {
        min_abs = abs_val;
        three_closest_sum = two_closest_sum + nums[i];
      }
    }
    return three_closest_sum;
  }
};

合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

我的解法，经典的双指针合并，用了额外空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
 public:
  void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    vector<int> nums1_copy(nums1.begin(), nums1.begin() + m);
    int i = 0;
    int j = 0;
    int k = 0;
    while (i < m && j < n) {
      if (nums1_copy[i] < nums2[j]) {
        nums1[k] = nums1_copy[i];
        i++;
        k++;
      } else {
        nums1[k] = nums2[j];
        j++;
        k++;
      }
    }
    while (i < m) {
      nums1[k] = nums1_copy[i];
      i++;
      k++;
    }
    while (j < n) {
      nums1[k] = nums2[j];
      j++;
      k++;
    }
  }
};

官方题解，同样使用双指针，但是逆向遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
 public:
  void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int i = m - 1;
    int j = n - 1;
    int k = m + n - 1;
    while (i >= 0 && j >= 0) {
      if (nums1[i] > nums2[j]) {
        nums1[k] = nums1[i];
        i--;
        k--;
      } else {
        nums1[k] = nums2[j];
        j--;
        k--;
      }
    }
    while (i >= 0) {
      nums1[k] = nums1[i];
      i--;
      k--;
    }
    while (j >= 0) {
      nums1[k] = nums2[j];
      j--;
      k--;
    }
  }
};

二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

我的解法，朴素的dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
 public:
  void dfs(TreeNode *node, int level, int *max_level) {
    if (node->left == nullptr && node->right == nullptr) {
      *max_level = max(*max_level, level);
      return;
    }
    if (node->left != nullptr) {
      dfs(node->left, level + 1, max_level);
    }
    if (node->right != nullptr) {
      dfs(node->right, level + 1, max_level);
    }
  }
  int maxDepth(TreeNode *root) {
    if (root == nullptr) {
      return 0;
    }
    int ans = 0;
    dfs(root, 1, &ans);
    return ans;
  }
};

简洁的官方题解，两行实现

1
2
3
4
5
6
7
class Solution {
 public:
  int maxDepth(TreeNode *root) {
    if (root == nullptr) return 0;
    return max(maxDepth(root->left), maxDepth(root->right)) + 1;
  }
};

连续子数组的最大和

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。

看到是简单题，就没想啥高深的方法，遍历一遍数组，维护局部最大连续和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
 public:
  int maxSubArray(vector<int>& nums) {
    int max_val = nums[0];
    int sum = 0;         // 连续和
    bool vaild = false;  // 连续和是否有效，边界情况即为全部负数
    for (int num : nums) {
      if (num < 0) {  // 连续和开始减小，需在之前保存状态
        if (vaild) {
          max_val = max(max_val, sum);
        } else {
          max_val = max(max_val, num);
        }
      }
      sum += num;
      vaild = true;
      if (sum < 0) {  // 重置连续和
        sum = 0;
        vaild = false;
      }
    }
    if (vaild) {  // 结束前进行一次判断
      max_val = max(max_val, sum);
    }
    return max_val;
  }
};

没想到官方题解竟然用到了动态规划的思想，虽然代码非常简单

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
 public:
  int maxSubArray(vector<int>& nums) {
    int max_val = nums[0];
    int pre = 0;
    for (int num : nums) {
      pre = max(pre + num, num);
      max_val = max(max_val, pre);
    }
    return max_val;
  }
};

二叉树中的最长交错路径

给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：

选择二叉树中 任意 节点和一个方向（左或者右）。
如果前进方向为右，那么移动到当前节点的的右子节点，否则移动到它的左子节点。
改变前进方向：左变右或者右变左。
重复第二步和第三步，直到你在树中无法继续移动。

交错路径的长度定义为：访问过的节点数目 - 1（单个节点的路径长度为 0 ）。
请你返回给定树中最长 交错路径 的长度。

没写出来，没理解题意，交错路径的末尾不一定是叶子节点，自己写的dfs超时了，抄的官方题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
 public:
  void dfs(TreeNode *node, int dir, int len) {
    max_len_ = max(max_len_, len);  // 记录当前最长交错路径
    if (dir == 0) {
      if (node->left != nullptr) {  // 向左子树前进，继续当前路径
        dfs(node->left, 1, len + 1);
      }
      if (node->right != nullptr) {  // 另开一个路径
        dfs(node->right, 0, 1);
      }
    }
    if (dir == 1) {
      if (node->left != nullptr) {  // 另开一个路径
        dfs(node->left, 1, 1);
      }
      if (node->right != nullptr) {  // 向右子树前进，继续当前路径
        dfs(node->right, 0, len + 1);
      }
    }
  }
  int longestZigZag(TreeNode *root) {
    if (root == nullptr) {
      return 0;
    }
    max_len_ = 0;
    dfs(root, 0, 0);
    dfs(root, 1, 0);
    return max_len_;
  }

 private:
  int max_len_;
};

验证二叉树的前序序列化

序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。
给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

利用前序遍历的特点，叶子节点的两个空节点一定紧紧挨着该叶子节点，所以可以将x # #格式的数据等价为#，即该叶子节点为空的序列，逆序遍历序列并一直利用这种方法消除节点，最终合法的前序遍历序列会归约到一个空节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
 public:
  bool isValidSerialization(string preorder) {
    int empty_node_cnt = 0;  // 空节点个数
    for (int i = preorder.length() - 1; i >= 0; i--) {
      if (preorder[i] == '#') {
        empty_node_cnt++;
      } else if (preorder[i] != ',') {
        if (empty_node_cnt < 2) {  // 没有足够的空节点
          return false;
        }
        empty_node_cnt--;                       // 合并节点，将x # #变为#
        while (i >= 0 && preorder[i] != ',') {  // 移动至前面的逗号处
          i--;
        }
      }
    }
    return empty_node_cnt == 1;  // 最终合并结果为一个空节点
  }
};

两句话中的不常见单词

句子 是一串由空格分隔的单词。每个 单词 仅由小写字母组成。
如果某个单词在其中一个句子中恰好出现一次，在另一个句子中却 没有出现 ，那么这个单词就是 不常见的 。
给你两个 句子 s1 和 s2 ，返回所有 不常用单词 的列表。返回列表中单词可以按 任意顺序 组织。

简单题，明显是分割字符串后加入哈希表，我采用的方法是使用find substr分割出单词，而官方题解利用stringstream来分割句子中的单词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
 public:
  vector<string> uncommonFromSentences(string s1, string s2) {
    s1.push_back(' ');  // 末尾加入空格，便于统一处理
    s2.push_back(' ');
    string_view view1(s1);
    string_view view2(s2);
    unordered_map<string_view, int> count;  // 单词与出现次数映射
    int last_pos = 0;
    int pos;
    while ((pos = view1.find(' ', last_pos)) != string::npos) {  // 切割字符串
      count[view1.substr(last_pos, pos - last_pos)]++;
      last_pos = pos + 1;
    }
    last_pos = 0;
    while ((pos = view2.find(' ', last_pos)) != string::npos) {  // 切割字符串
      count[view2.substr(last_pos, pos - last_pos)]++;
      last_pos = pos + 1;
    }
    vector<string> res;
    for (auto& kv : count) {
      if (kv.second == 1) {  // 将出现次数为1的单词加入结果集合
        res.emplace_back(string(kv.first));
      }
    }
    return res;
  }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<string> uncommonFromSentences(string s1, string s2) {
        unordered_map<string, int> freq;
        
        auto insert = [&](const string& s) {
            stringstream ss(s);
            string word;
            while (ss >> word) {
                ++freq[move(word)];
            }
        };

        insert(s1);
        insert(s2);

        vector<string> ans;
        for (const auto& [word, occ]: freq) {
            if (occ == 1) {
                ans.push_back(word);
            }
        }
        return ans;
    }
};

二叉树最底层最左边的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。

这个题很容易想到使用BFS或DFS，不过感觉BFS适合一点，实现时我将层级信息一并存储，并保证左子节点先加入队列，后通过比较当前层级信息来得到该层的第一个叶子节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
 public:
  int findBottomLeftValue(TreeNode *root) {
    queue<pair<TreeNode *, int>> q;  // 存储节点指针与相应层数
    q.emplace(root, 1);              // 放入根节点
    int max_level = 0;
    int left_value = 0;
    while (!q.empty()) {
      auto [node, level] = q.front();
      q.pop();
      if (level > max_level && node->left == nullptr && node->right == nullptr) {  // 叶子节点
        max_level = level;
        left_value = node->val;
      }
      if (node->left != nullptr) {         // 保证左子节点更早被访问
        q.emplace(node->left, level + 1);  // 层数加一
      }

      if (node->right != nullptr) {
        q.emplace(node->right, level + 1);
      }
    }
    return left_value;
  }
};

而官方题解则直接让右边的子节点先加入队列，省去大段的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        int ret;
        queue<TreeNode *> q;
        q.push(root);
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            if (p->right) {
                q.push(p->right);
            }
            if (p->left) {
                q.push(p->left);
            }
            ret = p->val;
        }
        return ret;
    }
};

删除子文件夹

你是一位系统管理员，手里有一份文件夹列表 folder，你的任务是要删除该列表中的所有 子文件夹，并以 任意顺序 返回剩下的文件夹。
如果文件夹 folder[i] 位于另一个文件夹 folder[j] 下，那么 folder[i] 就是 folder[j] 的 子文件夹 。
文件夹的「路径」是由一个或多个按以下格式串联形成的字符串：’/‘ 后跟一个或者多个小写英文字母。
例如，”/leetcode” 和 “/leetcode/problems” 都是有效的路径，而空字符串和 “/“ 不是。

没想到啥高深的方法，就直接对数组进行排序，而后依次判断各个文件夹是否为前面最后一个独立文件夹（即不是其他文件夹的子文件夹）的子文件夹。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
 public:
  bool isSubFolder(const string& s1, const string& s2) {  // s2是否为s1的子文件夹
    if (s1.length() >= s2.length()) {                     // 长度不符合要求
      return false;
    }
    int s1_len = s1.length();
    for (int i = 0; i < s1_len; i++) {
      if (s1[i] != s2[i]) {
        return false;
      }
    }
    return s2[s1_len] == '/';  // 前缀完全相同，还需下一个字符为分隔符，避免 /c  /ca的情况
  }
  vector<string> removeSubfolders(vector<string>& folder) {
    vector<string> res;
    int folder_size = folder.size();
    sort(folder.begin(), folder.end());  // 按ascii码排序，父文件夹一定在其子文件夹前面
    res.emplace_back(move(folder[0]));   // 第一个文件夹一定不是其他文件夹的子文件夹
    for (int i = 1; i < folder_size; i++) {
      if (!isSubFolder(res.back(), folder[i])) {  // 不是前面独立文件夹的子文件夹
        res.emplace_back(move(folder[i]));
      }
    }
    return res;
  }
};

官方题解给出了一种字典树的解法

字符串的好分割数目

题目简要
给你一个字符串 s ，一个分割被称为 「好分割」 当它满足：将 s 分割成 2 个字符串 p 和 q ，它们连接起来等于 s 且 p 和 q 中不同字符的数目相同。
请你返回 s 中好分割的数目。

看到是求数目，就排除了动态规划（一般是最优解问题），一时间没想到啥好方法，就直接顺序逆序两次遍历，然后利用集合的特性，得到不同字符的数目，最后进行一次比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
 public:
  int numSplits(string s) {
    int len = s.length();
    vector<int> left(len);
    vector<int> right(len);
    unordered_set<char> left_set;
    unordered_set<char> right_set;
    for (int i = 0; i < len; i++) {
      // 不包括当前字符
      left[i] = left_set.size();
      left_set.emplace(s[i]);
    }
    for (int i = len - 1; i >= 0; i--) {
      // 包括当前字符
      right_set.emplace(s[i]);
      right[i] = right_set.size();
    }
    int num = 0;
    for (int i = 0; i < len; i++) {
      if (left[i] > right[i]) {
        return num;
      } else if (left[i] == right[i]) {
        num++;
      }
    }
    return num;
  }
};

而官方题解则使用递推公式，利用了上一次的信息

类似的代码如下（没有使用官方题解的bitset）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
 public:
  int numSplits(string s) {
    int len = s.length();
    vector<int> left(len);
    vector<int> right(len);
    vector<bool> left_occur(26, false);
    vector<bool> right_occur(26, false);
    left[0] = 1;  // 第一个字符
    left_occur[s[0] - 'a'] = true;
    for (int i = 1; i < len; i++) {  // 从第二个字符开始
      if (left_occur[s[i] - 'a'] == true) {
        left[i] = left[i - 1];
      } else {
        left_occur[s[i] - 'a'] = true;
        left[i] = left[i - 1] + 1;
      }
    }
    right[len - 1] = 1;  // 倒数第一个字符
    right_occur[s[len - 1] - 'a'] = true;
    for (int i = len - 2; i >= 0; i--) {  // 从倒数第二个字符开始
      if (right_occur[s[i] - 'a'] == true) {
        right[i] = right[i + 1];
      } else {
        right_occur[s[i] - 'a'] = true;
        right[i] = right[i + 1] + 1;
      }
    }
    int num = 0;
    for (int i = 0; i < len - 1; i++) {
      if (left[i] > right[i + 1]) {
        return num;
      } else if (left[i] == right[i + 1]) {
        num++;
      }
    }
    return num;
  }
};

最接近目标价格的甜点成本

最接近目标价格的甜点成本
题目简要： 你打算做甜点，现在需要购买配料。目前共有 n 种冰激凌基料和 m 种配料可供选购。而制作甜点需要遵循以下几条规则：

  1. 必须选择 一种 冰激凌基料。
  2. 可以添加 一种或多种 配料，也可以不添加任何配料。
  3. 每种类型的配料 最多两份 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
 public:
  void comparePrice(int cost) {  // 比较得到绝对差值最小，同时成本最小的成本
    int diff = abs(cost - target_price);
    if (diff < min_target_diff || (diff == min_target_diff && cost < suit_price)) {
      min_target_diff = diff;
      suit_price = cost;
    }
  }
  void findCloseCost(vector<int>& toppingCosts, int start, int end, int cur_cost) {
    if (cur_cost > target_price || start > end) {  // 停止遍历条件
      comparePrice(cur_cost);
      return;
    }
    if (target_price - cur_cost < toppingCosts[start]) {             // 未加该配料与加一次配料位于目标价格两端
      comparePrice(cur_cost);                                        // 比较左端价格
    } else if (target_price - cur_cost < toppingCosts[start] * 2) {  // 加一次配料与加两次配料位于目标价格两端
      comparePrice(cur_cost + toppingCosts[start]);                  // 比较左端价格
    }
    findCloseCost(toppingCosts, start + 1, end, cur_cost);                            // 不选择该配料
    findCloseCost(toppingCosts, start + 1, end, cur_cost + toppingCosts[start]);      // 选择一次配料
    findCloseCost(toppingCosts, start + 1, end, cur_cost + toppingCosts[start] * 2);  // 选择两次配料
  }
  int closestCost(vector<int>& baseCosts, vector<int>& toppingCosts, int target) {
    min_target_diff = abs(baseCosts[0] - target);  // 选择第一个基料作为初始值
    suit_price = baseCosts[0];
    target_price = target;
    int top_size = toppingCosts.size();
    for (int base : baseCosts) {
      findCloseCost(toppingCosts, 0, top_size - 1, base);  // 深度搜索，找到最小差值
    }
    return suit_price;
  }

 private:
  int min_target_diff;  // 绝对差值
  int suit_price;       // 最终成本
  int target_price;     // 目标成本
};
  1. 不是所有的深度搜索都需要for循环
  2. 考虑边界条件，都大于或都小于

字符串中不同整数的数目

给你一个字符串 word ，该字符串由数字和小写英文字母组成。
请你用空格替换每个不是数字的字符。例如，”a123bc34d8ef34” 将会变成 “ 123 34 8 34” 。注意，剩下的这些整数为（相邻彼此至少有一个空格隔开）：”123”、”34”、”8” 和 “34” 。
返回对 word 完成替换后形成的 不同 整数的数目。
只有当两个整数的 不含前导零 的十进制表示不同， 才认为这两个整数也不同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  int numDifferentIntegers(string word) {
     unordered_set<string> numbers;  // 字符串中的数字
    int status = 0;       // 0 字母 1 数字
    int number_start;
    int number_end;
    char c;
    word.push_back('a');  // 保证最后一位一定为字符，简化处理流程
    int len = word.length();
    for (int i = 0; i < len; i++) {
      c = word[i];
      if (status == 0 && (c >= '0' && c <= '9')) {  // 遇到第一位数字，状态转换
        status = 1;
        number_start = i;
      } else if (status == 1 && !(c >= '0' && c <= '9')) {  // 遇到字母，计算数字字符串，状态转换
        number_end = i - 1;
        status = 0;
        while (number_start <= number_end && word[number_start] == '0') {  // 去除前导0
          number_start++;
        }
        if (number_start > number_end) {  // 如果全为0
          numbers.emplace("0");
        } else {  // 将数字字符串加入结果集合
          numbers.emplace(word.substr(number_start, number_end - number_start + 1));
        }
      }
    }
    return numbers.size();
  }
};

注意整数溢出

通过最少操作次数使数组的和相等

题目简要
给你两个长度可能不等的整数数组 nums1 和 nums2 。两个数组中的所有值都在 1 到 6 之间（包含 1 和 6）。
每次操作中，你可以选择 任意 数组中的任意一个整数，将它变成 1 到 6 之间 任意 的值（包含 1 和 6）。
请你返回使 nums1 中所有数的和与 nums2 中所有数的和相等的最少操作次数。如果无法使两个数组的和相等，请返回 -1 。

我的解法（不咋行）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
const int kInf = 0x7fffffff;
class Solution {
 public:
  int minOperations(vector<int>& nums1, vector<int>& nums2) {
    int size1 = nums1.size();
    int size2 = nums2.size();
    int max_size = max(size1, size2);
    int min_size = min(size1, size2);
    int possible_value_start = max_size;
    int possible_value_end = min_size * 6;
    if (possible_value_start > possible_value_end) {  // 两数组取值范围不交叉
      return -1;
    }
    // 计算两数组之和
    int sum1 = 0;
    int sum2 = 0;
    for (int num : nums1) {
      sum1 += num;
    }
    for (int num : nums2) {
      sum2 += num;
    }
    if (sum1 == sum2) {  // 所有数之和已相等，直接发挥
      return 0;
    }
    // 所有数之和可能范围
    possible_value_start = max(min(sum1, sum2), possible_value_start);
    possible_value_end = min(max(sum1, sum2), possible_value_end);
    sort(nums1.begin(), nums1.end());
    sort(nums2.begin(), nums2.end());
    // 到某个数的操作次数
    vector<int> dist1(size1 * 6 + 1);
    vector<int> dist2(size2 * 6 + 1);
    dist1[sum1] = 0;
    dist2[sum2] = 0;
    int index, next_index;
    if (sum1 <= possible_value_start) {  // 数组1逐渐增大，数组2逐渐减小
      index = sum1 + 1;
      for (int i = 1; i <= size1; i++) {  // 贪心策略：将第i小的数变成6
        next_index = index + 6 - nums1[i - 1];
        for (int j = index; j < next_index; j++) {
          dist1[j] = i;
        }
        index = next_index;
        if (index > possible_value_end) {  // 提前退出
          break;
        }
      }
      index = sum2 - 1;
      for (int i = 1; i <= size2; i++) {  // 贪心策略：将第i大的数变成1
        next_index = index - nums2[size2 - i] + 1;
        for (int j = index; j > next_index; j--) {
          dist2[j] = i;
        }
        index = next_index;
        if (index < possible_value_start) {  // 提前退出
          break;
        }
      }
    } else {  // 数组1逐渐减小，数组2逐渐增大
      index = sum2 + 1;
      for (int i = 1; i <= size2; i++) {
        next_index = index + 6 - nums2[i - 1];
        for (int j = index; j < next_index; j++) {
          dist2[j] = i;
        }
        index = next_index;
        if (index > possible_value_end) {
          break;
        }
      }
      index = sum1 - 1;
      for (int i = 1; i <= size1; i++) {
        next_index = index - nums1[size1 - i] + 1;
        for (int j = index; j > next_index; j--) {
          dist1[j] = i;
        }
        index = next_index;
        if (index < possible_value_start) {
          break;
        }
      }
    }
    int min_times = size1 + size2;
    for (int i = possible_value_start; i <= possible_value_end; i++) {  // 计算操作次数之和最小的所有数之和
      min_times = min(min_times, dist1[i] + dist2[i]);
    }
    return min_times;
  }
};

参考解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
 public:
  int minOperations(vector<int>& nums1, vector<int>& nums2) {
    int size1 = nums1.size();
    int size2 = nums2.size();
    int max_size = max(size1, size2);
    int min_size = min(size1, size2);
    int possible_value_start = max_size;
    int possible_value_end = min_size * 6;
    if (possible_value_start > possible_value_end) {  // 两数组取值范围不交叉
      return -1;
    }
    // 计算当前所有数之和
    int sum1 = accumulate(nums1.begin(), nums1.end(), 0);
    int sum2 = accumulate(nums2.begin(), nums2.end(), 0);
    int diff = sum1 - sum2;
    if (diff == 0) {
      return 0;
    }
    if (diff < 0) {  // 保证数组1之和大于数组2之和
      swap(nums1, nums2);
      diff = -diff;
    }
    // 计算每个数的贡献  cnt[i]表示贡献为i的个数
    int cnt[6] = {0};
    for (int num : nums1) {  // 将每个数变成1
      cnt[num - 1]++;
    }
    for (int num : nums2) {  // 将每个数变成6
      cnt[6 - num]++;
    }
    int times = 0;
    for (int i = 5; i >= 1; i--) {    // 贪心：从贡献大的数开始变化
      if (diff - i * cnt[i] <= 0) {   // 变化这些数可以使所有数之和相等
        times += (diff + i - 1) / i;  // 向上取整（例：差值为10，需要4个贡献为3的数）
        return times;
      }
      // 积累这些数的贡献，叠加次数
      diff -= i * cnt[i];
      times += cnt[i];
    }
    return -1;
  }
};

参考解法比我的解法简洁的点在于：
1 通过swap保证nums1与nums2的相对关系
2 由于可能的贡献只有6个，可直接用数组存各贡献的次数，而不需要排序
3 将两个数组的贡献放在一起考虑，而不是独立考虑然后遍历可能范围两数之和

还原排列的最少操作步数

题目简要
给你一个偶数 n​​​​​​ ，已知存在一个长度为 n 的排列 perm ，其中 perm[i] == i​（下标 从 0 开始 计数）。

一步操作中，你将创建一个新数组 arr ，对于每个 i ：
如果 i % 2 == 0 ，那么 arr[i] = perm[i / 2]
如果 i % 2 == 1 ，那么 arr[i] = perm[n / 2 + (i - 1) / 2]
然后将 arr​​ 赋值​​给 perm 。

要想使 perm 回到排列初始值，至少需要执行多少步操作？返回最小的 非零 操作步数。

我开始想找规律，但看了看没找到，就直接模拟了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
 public:
  bool check(const vector<int>& vec) {
    int size = vec.size();
    for (int i = 0; i < size; i++) {
      if (vec[i] != i) {
        return false;
      }
    }
    return true;
  }
  int reinitializePermutation(int n) {
    vector<vector<int>> arr(2, vector<int>(n));
    for (int i = 0; i < n; i++) {
      arr[0][i] = i;
    }
    int times = 0;
    int src = 1;
    int des = 0;
    do {
      times++;
      swap(src, des);
      for (int i = 0; i < n; i++) {
        arr[des][i] = (i % 2 == 0) ? arr[src][i / 2] : arr[src][n / 2 + (i - 1) / 2];
      }
    } while (!check(arr[des]));
    return times;
  }
};

参考解法

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
 public:
  int reinitializePermutation(int n) {
    int times = 0;
    int i = 1;
    do {
      i = i % 2 == 0 ? i / 2 : (n + i - 1) / 2;
      times++;
    } while (i != 1);
    return times;
  }
};

句子相似性 III

题目简要
一个句子是由一些单词与它们之间的单个空格组成，且句子的开头和结尾没有多余空格。比方说，”Hello World” ，”HELLO” ，”hello world hello world” 都是句子。每个单词都 只 包含大写和小写英文字母。

如果两个句子 sentence1 和 sentence2 ，可以通过往其中一个句子插入一个任意的句子（可以是空句子）而得到另一个句子，那么我们称这两个句子是 相似的 。比方说，sentence1 = “Hello my name is Jane” 且 sentence2 = “Hello Jane” ，我们可以往 sentence2 中 “Hello” 和 “Jane” 之间插入 “my name is” 得到 sentence1 。

给你两个句子 sentence1 和 sentence2 ，如果 sentence1 和 sentence2 是相似的，请你返回 true ，否则返回 false 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class Solution {
 public:
  vector<string> split(string& s) {
    vector<string> res;
    s += ' ';  // 在尾部加上空格，统一处理
    size_t last_pos = 0;
    size_t pos = 0;
    while (pos != string::npos) {
      pos = s.find(' ', last_pos);
      if (pos != string::npos) {
        res.emplace_back(s.substr(last_pos, pos - last_pos));  // 记录单词
        last_pos = pos + 1;
      }
    }
    return res;
  }
  bool areSentencesSimilar(string sentence1, string sentence2) {
    if (sentence1.length() > sentence2.length()) {  // 保证第一个字符串短于第二个
      swap(sentence1, sentence2);
    }
    vector<string> strs1 = split(sentence1);
    vector<string> strs2 = split(sentence2);
    int i = 0;
    int j = strs1.size() - 1;
    int k = strs2.size() - 1;
    while (i < strs1.size() && strs1[i] == strs2[i]) {
      i++;
    }
    while (j >= 0 && strs1[j] == strs2[k]) {
      j--;
      k--;
    }
    return i > j;
  }
};

// 使用string_view的版本
class Solution {
 public:
  vector<string_view> split(string& str) {
    vector<string_view> res;
    str += ' ';  // 在尾部加上空格，统一处理
    string_view s(str);
    size_t last_pos = 0;
    size_t pos = 0;
    while (pos != string::npos) {
      pos = s.find(' ', last_pos);
      if (pos != string::npos) {
        res.emplace_back(s.substr(last_pos, pos - last_pos));  // 记录单词
        last_pos = pos + 1;
      }
    }
    return res;
  }
  bool areSentencesSimilar(string sentence1, string sentence2) {
    if (sentence1.length() > sentence2.length()) {  // 保证第一个字符串短于第二个
      swap(sentence1, sentence2);
    }
    vector<string_view> strs1 = split(sentence1);
    vector<string_view> strs2 = split(sentence2);
    int i = 0;
    int j = strs1.size() - 1;
    int k = strs2.size() - 1;
    while (i < strs1.size() && strs1[i] == strs2[i]) {
      i++;
    }
    while (j >= 0 && strs1[j] == strs2[k]) {
      j--;
      k--;
    }
    return i > j;
  }
};

与官方题解相比运行时间有较大差距，主要在于对string_view类型的应用

std::string_view类的成员变量只包含两个：字符串指针和字符串长度。字符串指针可能是某个连续字符串的其中一段的指针，而字符串长度也不一定是整个字符串长度，也有可能是某个字符串的一部分长度。std::string_view所实现的接口中，完全包含了std::string的所有只读的接口，所以在很多场合可以轻易使用std::string_view代替std::string。一个通常的用法是，生成一个std::string后，如果后续的操作不再对其进行修改，那么可以考虑把std::string转换成为std::string_view，后续操作全部使用std::string_view来进行，这样字符串的传递变得轻量级。

C++17剖析：string_view的实现，以及性能

统计网格图中没有被保卫的格子数

题目简要
给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ，其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ，分别表示第 i 个警卫和第 j 座墙所在的位置。
一个警卫能看到 4 个坐标轴方向（即东、南、西、北）的 所有 格子，除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到，那么我们说这个格子被 保卫 了。
请你返回空格子中，有多少个格子是 没被保卫 的。

暴力枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
 public:
  int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
    // 0 未受保护 1 受保护 -1 警卫 -2 墙
    vector<vector<int>> arr(m, vector<int>(n, 0));  // 空白格
    for (auto& guard : guards) {
      arr[guard[0]][guard[1]] = -1;
    }
    for (auto& wall : walls) {
      arr[wall[0]][wall[1]] = -2;
    }

    int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    int protected_block = 0;
    for (auto& guard : guards) {
      for (int i = 0; i < 4; i++) {
        int x = guard[0];
        int y = guard[1];
        int next_x = x + dir[i][0];
        int next_y = y + dir[i][1];
        while (next_x >= 0 && next_x < m && next_y >= 0 && next_y < n && arr[next_x][next_y] >= 0) {  // 坐标合法且未遇到墙/警卫
          if (arr[next_x][next_y] == 0) {
            protected_block++;
          }
          x = next_x;
          y = next_y;
          arr[x][y] = 1;  // 给空白格赋值
          next_x = x + dir[i][0];
          next_y = y + dir[i][1];
        }
      }
    }
    int unprotected_num = m * n - guards.size() - walls.size() - protected_block;
    return unprotected_num;
  }
};

官方题解——广度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
 public:
  int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
    // 0 未受保护 -1 警卫 -2 墙  以前四位作为各方向访问记录
    vector<vector<int>> arr(m, vector<int>(n, 0));  // 空白格
    queue<tuple<int, int, int>> q;
    for (auto& guard : guards) {
      arr[guard[0]][guard[1]] = -1;
      for (int dir = 0; dir < 4; ++dir) {
        q.emplace(guard[0], guard[1], dir);
      }
    }
    for (auto& wall : walls) {
      arr[wall[0]][wall[1]] = -2;
    }

    int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    int protected_block = 0;
    while (!q.empty()) {
      auto [x, y, dir] = q.front();
      q.pop();
      int nx = x + directions[dir][0];
      int ny = y + directions[dir][1];
      if (nx >= 0 && nx < m && ny >= 0 && ny < n && arr[nx][ny] >= 0 && (arr[nx][ny] & (1 << dir)) == 0) {  // 坐标合法且为未被访问的空白格
        if (arr[nx][ny] == 0) {                                                                             // 第一次访问
          protected_block++;
        }
        arr[nx][ny] |= (1 << dir);
        q.emplace(nx, ny, dir);
      }
    }
    int unprotected_num = m * n - guards.size() - walls.size() - protected_block;
    return unprotected_num;
  }
};

非常漂亮的思路，另外注意& ==的运算符优先级

最大二叉树与单调栈

题目简要
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
思路
按照题目步骤，实现简单的递归函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
 public:
  // 左闭右开区间
  TreeNode *impl(vector<int> &nums, vector<int>::iterator begin, vector<int>::iterator end) {
    if (begin >= end) {
      return nullptr;
    }
    vector<int>::iterator max_pos = max_element(begin, end);
    TreeNode *node = new TreeNode(*max_pos);
    node->left = impl(nums, begin, max_pos);  // 注意为max_pos而不是max_pos-1
    node->right = impl(nums, max_pos + 1, end);
    return node;
  }
  TreeNode *constructMaximumBinaryTree(vector<int> &nums) { return impl(nums, nums.begin(), nums.end()); }
};

看完官方题解，竟然还能用所谓的单调栈求解，阅读一篇相关博客特殊数据结构：单调栈
简单写完496. 下一个更大元素 I与503. 下一个更大元素 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// 496
class Solution {
 public:
  vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
    stack<int> s;
    unordered_map<int, int> next;  // 当前值与更大值映射

    for (int i = nums2.size() - 1; i >= 0; i--) {
      while (!s.empty() && s.top() < nums2[i]) {  // 弹出比其小的元素
        s.pop();
      }
      int next_value = s.empty() ? -1 : s.top();  // 下一个更大的元素
      next.insert({nums2[i], next_value});
      s.emplace(nums2[i]);
    }

    vector<int> ans(nums1.size());
    for (int i = 0; i < nums1.size(); i++) {
      ans[i] = next[nums1[i]];
    }
    return ans;
  }
};
// 503
class Solution {
 public:
  vector<int> nextGreaterElements(vector<int>& nums) {
    vector<int> ans(nums.size());
    stack<int> st;
    // 进行两次遍历
    for (int i = nums.size() - 1; i >= 0; --i) {
      while (!st.empty() && st.top() <= nums[i]) {
        st.pop();
      }
      st.emplace(nums[i]);
    }
    // 此时已有从栈顶至栈底递增的数组元素
    for (int i = nums.size() - 1; i >= 0; --i) {
      while (!st.empty() && st.top() <= nums[i]) {
        st.pop();
      }
      ans[i] = st.empty() ? -1 : st.top();
      st.emplace(nums[i]);
    }
    return ans;
  }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
 public:
  TreeNode *constructMaximumBinaryTree(vector<int> &nums) {
    int n = nums.size();
    stack<int> st;
    vector<int> left(n, -1), right(n, -1);  // 左右两侧更大元素索引，初始为-1
    vector<TreeNode *> tree(n);             // 指针数组
    for (int i = 0; i < n; ++i) {
      tree[i] = new TreeNode(nums[i]);  // 创建节点
      // 维持栈顶至栈底递增关系
      while (!st.empty() && nums[i] > nums[st.top()]) {  // 若栈顶元素比当前元素小
        right[st.top()] = i;                             // 栈顶元素的右侧更大元素索引为i
        st.pop();                                        // 弹出栈顶元素
      }
      if (!st.empty()) {  // 若栈非空，则栈顶元素为左侧更大元素索引
        left[i] = st.top();
      }
      st.emplace(i);
    }

    TreeNode *root = nullptr;
    // nums[i] 的父结点是两个边界中较小的那个元素对应的节点。
    for (int i = 0; i < n; ++i) {
      if (left[i] == -1 && right[i] == -1) {  // 最大元素，即为根节点
        root = tree[i];
      } else if (right[i] == -1 || (left[i] != -1 && nums[left[i]] < nums[right[i]])) {  // 左侧的元素较小，那么该元素就是左侧元素的右子节点
        tree[left[i]]->right = tree[i];
      } else {  // 右侧的元素较小，那么该元素就是右侧元素的左子节点。
        tree[right[i]]->left = tree[i];
      }
    }
    return root;
  }
};

和为s的连续正数序列

题目简要
输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。
序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

思路
刚开始想通过数学方法解出来，想了一会没想到，就直接暴力枚举了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  vector<vector<int>> findContinuousSequence(int target) {
    vector<vector<int>> res;
    const int max_begin = target / 2;
    for (int i = 1; i <= max_begin; i++) {
      int num = i;
      int sum = target;
      while (sum > 0) {  // 依次减去后面的数
        sum -= num;
        num++;
      }
      if (sum == 0) {  // 为该序列之和
        vector<int> arr;
        arr.reserve(num - i);  // 预订空间
        for (int j = i; j < num; j++) {
          arr.emplace_back(j);
        }
        res.emplace_back(move(arr));  // 加入结果集
      }
    }
    return res;
  }
};

看到官方题解双指针/滑动窗口解题，mark一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  vector<vector<int>> findContinuousSequence(int target) {
    vector<vector<int>> vec;
    vector<int> res;
    for (int l = 1, r = 2; l < r;) {
      int sum = (l + r) * (r - l + 1) / 2;
      if (sum == target) {
        res.clear();
        for (int i = l; i <= r; ++i) {
          res.emplace_back(i);
        }
        vec.emplace_back(res);
        l++;
      } else if (sum < target) {
        r++;
      } else {
        l++;
      }
    }
    return vec;
  }
};

LFU 缓存

题目简要
请你为 最不经常使用（LFU）缓存算法设计并实现数据结构。

实现 LFUCache 类：

LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键 key 存在于缓存中，则获取键的值，否则返回 -1 。
void put(int key, int value) - 如果键 key 已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量 capacity 时，则应该在插入新项之前，移除最不经常使用的项。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最近最久未使用 的键。
为了确定最不常使用的键，可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

思路
刚开始我想的是使用LRU实现类似的方式，用一个双向链表存放数据，用一个哈希表记录数据位置，加速查找，但提交后超出时间限制。
我的实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
struct DataNode {  // 数据节点
  int key_;
  int value_;
  int count_;
  DataNode(int key, int value, int count) : key_(key), value_(value), count_(count) {}
};

class LFUCache {
 public:
  LFUCache(int capacity) : size_(0), capacity_(capacity) {}

  int get(int key) {
    if (capacity_ <= 0) {
      return -1;
    }
    auto iter = speed_map_.find(key);
    if (iter == speed_map_.end()) {
      return -1;
    }
    list<DataNode>::iterator pos = iter->second;
    DataNode new_node = *pos;
    new_node.count_++;
    auto new_pos = data_.erase(pos);  // 找到新的插入位置(大于该count或末尾)
    while (new_pos != data_.end() && new_pos->count_ <= new_node.count_) {
      ++new_pos;
    }
    speed_map_[key] = data_.insert(new_pos, new_node);
    return new_node.value_;
  }

  void put(int key, int value) {
    if (capacity_ <= 0) {
      return;
    }
    auto iter = speed_map_.find(key);
    if (iter == speed_map_.end()) {
      if (size_ == capacity_) {  // 淘汰头部的数据节点
        speed_map_.erase(data_.front().key_);
        data_.pop_front();
        size_--;
      }
      // 插入新节点
      DataNode node(key, value, 1);
      auto pos = data_.begin();
      while (pos != data_.end() && pos->count_ <= 1) {
        ++pos;
      }
      speed_map_.insert({key, data_.insert(pos, node)});
      size_++;
    } else {
      // 更新节点
      list<DataNode>::iterator pos = iter->second;
      DataNode new_node = *pos;
      new_node.value_ = value;
      new_node.count_++;
      auto new_pos = data_.erase(pos);
      while (new_pos != data_.end() && new_pos->count_ <= new_node.count_) {
        ++new_pos;
      }
      speed_map_[key] = data_.insert(new_pos, new_node);
    }
  }

 private:
  int size_;
  int capacity_;
  list<DataNode> data_;                                     // 存放数据节点，越靠前越容易被淘汰
  unordered_map<int, list<DataNode>::iterator> speed_map_;  // 加速查找
};

LFU与LRU不同的是，它并不是每次都会插入至队首或队尾，故更新节点位置时需要进行遍历，为此，就不能用链表作为存放数据的数据结构，而是平衡二叉树（set）
官方题解1大致实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
struct DataNode {  // 数据节点
  int key_;
  int value_;
  int count_;        // 出现次数
  int insert_time_;  // 插入时间
  DataNode(int key, int value, int count, int insert_time) : key_(key), value_(value), count_(count), insert_time_(insert_time) {}
  bool operator<(const DataNode& node) const { return count_ < node.count_ || (count_ == node.count_ && insert_time_ < node.insert_time_); }  // 自定义排序函数
};

class LFUCache {
 public:
  LFUCache(int capacity) : capacity_(capacity), timer_(0) {}
  int get(int key) {
    if (capacity_ <= 0) {
      return -1;
    }
    auto iter = position_.find(key);
    if (iter == position_.end()) {  // key不存在
      return -1;
    }
    // 更新节点信息
    auto pos = iter->second;
    DataNode new_node(key, pos->value_, pos->count_ + 1, timer_++);
    data_.erase(pos);
    position_[key] = data_.emplace(new_node).first;
    return new_node.value_;
  }

  void put(int key, int value) {
    if (capacity_ <= 0) {
      return;
    }
    auto iter = position_.find(key);
    if (iter == position_.end()) {      // 插入数据
      if (data_.size() == capacity_) {  // 达到容量，淘汰数据
        auto evict_pos = data_.begin();
        position_.erase(evict_pos->key_);
        data_.erase(evict_pos);
      }
      DataNode new_node(key, value, 1, timer_++);
      position_.insert({key, data_.emplace(new_node).first});
    } else {  // 更新数据
      auto pos = iter->second;
      DataNode new_node(key, value, pos->count_ + 1, timer_++);
      data_.erase(pos);
      position_[key] = data_.emplace(new_node).first;
    }
  }

 private:
  int capacity_;
  int timer_;                                             // 逻辑计数器
  set<DataNode> data_;                                    // 以红黑树存放数据节点
  unordered_map<int, set<DataNode>::iterator> position_;  // 数据位置
};

DataNode包含key是为了淘汰时删除map中的数据。虽然题解1可以通过测试，但复杂度在对数级。题解2则使用两个哈希表，将复杂度降到了常数级。
实际上题解2相当于使用两个哈希表将LFU分成了不同出现次数的LRU。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
// 缓存的节点信息
struct Node {
  int key, val, freq;
  Node(int _key, int _val, int _freq) : key(_key), val(_val), freq(_freq) {}
};
class LFUCache {
  int minfreq, capacity;
  unordered_map<int, list<Node>::iterator> key_table;
  unordered_map<int, list<Node>> freq_table;

 public:
  LFUCache(int _capacity) {
    minfreq = 0;
    capacity = _capacity;
    key_table.clear();
    freq_table.clear();
  }

  int get(int key) {
    if (capacity == 0) return -1;
    auto it = key_table.find(key);
    if (it == key_table.end()) return -1;
    list<Node>::iterator node = it->second;
    int val = node->val, freq = node->freq;
    freq_table[freq].erase(node);
    // 如果当前链表为空，我们需要在哈希表中删除，且更新minFreq
    if (freq_table[freq].size() == 0) {
      freq_table.erase(freq);
      if (minfreq == freq) minfreq += 1;
    }
    // 插入到 freq + 1 中
    freq_table[freq + 1].emplace_front(Node(key, val, freq + 1));
    key_table[key] = freq_table[freq + 1].begin();
    return val;
  }

  void put(int key, int value) {
    if (capacity == 0) return;
    auto it = key_table.find(key);
    if (it == key_table.end()) {
      // 缓存已满，需要进行删除操作
      if (key_table.size() == capacity) {
        // 通过 minFreq 拿到 freq_table[minFreq] 链表的末尾节点
        auto it2 = freq_table[minfreq].back();
        key_table.erase(it2.key);
        freq_table[minfreq].pop_back();
        if (freq_table[minfreq].size() == 0) {
          freq_table.erase(minfreq);
        }
      }
      freq_table[1].emplace_front(Node(key, value, 1));
      key_table[key] = freq_table[1].begin();
      minfreq = 1;
    } else {
      // 与 get 操作基本一致，除了需要更新缓存的值
      list<Node>::iterator node = it->second;
      int freq = node->freq;
      freq_table[freq].erase(node);
      if (freq_table[freq].size() == 0) {
        freq_table.erase(freq);
        if (minfreq == freq) minfreq += 1;
      }
      freq_table[freq + 1].emplace_front(Node(key, value, freq + 1));
      key_table[key] = freq_table[freq + 1].begin();
    }
  }
};

螺旋矩阵 II

题目简要
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

开始想找规律，找到坐标与值的关系，没找到就直接模拟，刚开始用递归实现，先赋值外圈，再赋值内圈，后面直接改成非递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
// 递归实现
const int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
class Solution {
 public:
  void computeNumber(vector<vector<int>>& vec, int start_x, int start_y, int start_value, int dim) {
    if (dim == 0) {
      return;
    }
    if (dim == 1) {
      vec[start_x][start_y] = start_value;
      return;
    }
    int i = start_x;
    int j = start_y;
    int x = start_value;
    int times = dim * dim - (dim - 2) * (dim - 2) - 1;  // 对外围赋值次数
    int cur_dir = 0;
    vec[i][j] = x++;
    while (times--) {
      i += dir[cur_dir][0];
      j += dir[cur_dir][1];
      vec[i][j] = x++;
      // 遇到边界，转向
      if (i == start_x && j == start_y + dim - 1) {
        cur_dir = 1;
      } else if (i == start_x + dim - 1 && j == start_y + dim - 1) {
        cur_dir = 2;
      } else if (i == start_x + dim - 1 && j == start_y) {
        cur_dir = 3;
      }
    }
    // 对内圈赋值
    computeNumber(vec, start_x + 1, start_y + 1, x, dim - 2);
  }
  vector<vector<int>> generateMatrix(int n) {
    vector<vector<int>> arr(n, vector<int>(n));
    computeNumber(arr, 0, 0, 1, n);
    return arr;
  }
};
// 非递归实现
const int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
class Solution {
 public:
  vector<vector<int>> generateMatrix(int n) {
    vector<vector<int>> vec(n, vector<int>(n));
    int dim = n;
    int start_x = 0;
    int start_y = 0;
    int i = 0;
    int j = 0;
    int x = 1;
    int cur_dir = 0;
    vec[i][j] = x++;
    int times = dim * dim - 1;
    while (times--) {
      i += dir[cur_dir][0];
      j += dir[cur_dir][1];
      vec[i][j] = x++;
      if (i == start_x && j == start_y + dim - 1) {
        cur_dir = 1;
      } else if (i == start_x + dim - 1 && j == start_y + dim - 1) {
        cur_dir = 2;
      } else if (i == start_x + dim - 1 && j == start_y) {
        cur_dir = 3;
      } else if (i == start_x + 1 && j == start_y) {
        // 进入内圈，转向
        cur_dir = 0;
        start_x++;
        start_y++;
        dim -= 2;
      }
    }
    return vec;
  }
};

官方题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int maxNum = n * n;
        int curNum = 1;
        vector<vector<int>> matrix(n, vector<int>(n));
        int row = 0, column = 0;
        vector<vector<int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};  // 右下左上
        int directionIndex = 0;
        while (curNum <= maxNum) {
            matrix[row][column] = curNum;
            curNum++;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= n || nextColumn < 0 || nextColumn >= n || matrix[nextRow][nextColumn] != 0) {
                directionIndex = (directionIndex + 1) % 4;  // 顺时针旋转至下一个方向
            }
            row = row + directions[directionIndex][0];
            column = column + directions[directionIndex][1];
        }
        return matrix;
    }
};

我的解法远没有官方题解简洁，关键在于官方题解抓住了若不为 0，则说明已经访问过此位置。 的性质，减去了四角边界的检查。

最大整除子集

题目简要：
给你一个由 无重复 正整数组成的集合 nums ，请你找出并返回其中最大的整除子集 answer ，子集中每一元素对 (answer[i], answer[j]) 都应当满足：
answer[i] % answer[j] == 0 ，或
answer[j] % answer[i] == 0
如果存在多个有效解子集，返回其中任何一个均可。

这个题目很容易看出是要使用动态规划解决，状态转移方程也比较容易看出，比较简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
 public:
  vector<int> largestDivisibleSubset(vector<int>& nums) {
    int nums_size = nums.size();
    vector<int> dp(nums_size, 1);  // 以第i位数结尾的最大整除子集长度
    dp[0] = 1;
    sort(nums.begin(), nums.end());  // 对数组进行排序
    for (int i = 1; i < nums_size; i++) {
      for (int j = 0; j < i; j++) {
        if (nums[i] % nums[j] == 0) {  // 尝试将第i位数字放在第j位数字后
          dp[i] = max(dp[i], dp[j] + 1);
        }
      }
    }
    auto max_iter = max_element(dp.begin(), dp.end());  // 找到最大整除子集长度
    if (*max_iter == 1) {                               // 题目未表达清晰此时应返回何值
      return {nums[0]};
    }
    // 倒推得到最大整除子集
    int end = max_iter - dp.begin();
    int count = *max_iter;         // 尚未加入集合数字的数目
    int cur_multiple = nums[end];  // 下一个加入的数需被该数整除
    vector<int> ans;
    for (int i = end; i >= 0; i--) {
      if (cur_multiple % nums[i] == 0 && dp[i] == count) {  // 符合条件，加入集合
        ans.emplace_back(nums[i]);
        cur_multiple = nums[i];
        count--;
      }
      if (count == 0) {
        return ans;
      }
    }
    return ans;
  }
};

非重叠矩形中的随机点

题目简要：
给定一个由非重叠的轴对齐矩形的数组 rects ，其中 rects[i] = [ai, bi, xi, yi] 表示 (ai, bi) 是第 i 个矩形的左下角点，(xi, yi) 是第 i 个矩形的右上角点。设计一个算法来随机挑选一个被某一矩形覆盖的整数点。矩形周长上的点也算做是被矩形覆盖。所有满足要求的点必须等概率被返回。

在给定的矩形覆盖的空间内的任何整数点都有可能被返回。

我刚开始就直接用点数组存储所有矩阵中的点，对于每个矩阵都进行两层循环遍历，但提交后显示超时，故计算矩阵总面积，或者说将所有整数点抽象成一条直线，先计算直线的总长度，在直线范围内随机选择一点，而后找到与其相对应的点坐标。虽然我刚开始使用了矩阵面积的前缀和辅助计算，但由于不怎么熟悉c++二分查找的相关函数，没有使用二分查找的方法加速查找。
最终代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
 public:
  Solution(vector<vector<int>>& rects) {
    int rect_size = rects.size();
    area_cusum = vector<int>(rect_size);
    // 计算面积累加和
    area_cusum[0] = (rects[0][2] - rects[0][0] + 1) * (rects[0][3] - rects[0][1] + 1);
    for (int i = 1; i < rect_size; i++) {
      int area = (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);
      area_cusum[i] = area_cusum[i - 1] + area;
    }
    area_sum = area_cusum[rect_size - 1];
    this->rects = move(rects);
  }

  vector<int> pick() {
    int index = rand() % area_sum;
    // 找到第一个大于index的矩阵索引
    int i = upper_bound(area_cusum.begin(), area_cusum.end(), index) - area_cusum.begin();
    int rect_index = (i == 0) ? index : index - area_cusum[i - 1];
    int x = rect_index % (rects[i][2] - rects[i][0] + 1) + rects[i][0];
    int y = rect_index / (rects[i][2] - rects[i][0] + 1) + rects[i][1];
    return {x, y};
  }

 private:
  vector<vector<int>> rects;
  vector<int> area_cusum;  // 累计和
  int area_sum;            // 总面积
};

C++ 语言基础 —— STL —— 算法 —— 二分查找算法

模拟行走机器人

题目简要：
机器人在一个无限大小的 XY 网格平面上行走，从点 (0, 0) 处开始出发，面向北方。该机器人可以接收以下三种类型的命令 commands ：
-2 ：向左转 90 度
-1 ：向右转 90 度
1 <= x <= 9 ：向前移动 x 个单位长度
在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。
机器人无法走到障碍物上，它将会停留在障碍物的前一个网格方块上，但仍然可以继续尝试进行该路线的其余部分。
返回从原点到机器人所有经过的路径点（坐标为整数）的最大欧式距离的平方。（即，如果距离为 5 ，则返回 25 ）

我的解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
class Solution {
 public:
  int robotSim(vector<int>& commands, vector<vector<int>>& obstacles) {
    map<int, set<int>> obstacle_x;  // 存入x坐标相同的y坐标 set有序
    map<int, set<int>> obstacle_y;  // 存入y坐标相同的y坐标 set有序
    for (auto& obstacle : obstacles) {
      if (obstacle_x.count(obstacle[0]) == 0) {
        obstacle_x[obstacle[0]] = {obstacle[1]};
      } else {
        obstacle_x[obstacle[0]].emplace(obstacle[1]);
      }
      if (obstacle_y.count(obstacle[1]) == 0) {
        obstacle_y[obstacle[1]] = {obstacle[0]};
      } else {
        obstacle_y[obstacle[1]].emplace(obstacle[0]);
      }
    }
    int dir[4][2] = {{1, 0}, {0, -1}, {-1, 0}, {0, 1}};  // 东 南 西 北
    int index = 3;
    int x = 0;
    int y = 0;
    int max_dist = 0;
    int next_x;
    int next_y;
    for (int cmd : commands) {
      switch (cmd) {
        case -1:
          index = (index + 1) % 4;  // 右转90度
          break;
        case -2:
          index = (index + 3) % 4;  // 左转90度
          break;
        default:
          next_x = x + dir[index][0] * cmd;
          next_y = y + dir[index][1] * cmd;
          switch (index) {
            case 0:  // 向东 顺序遍历
              if (obstacle_y.count(y) != 0) {
                for (auto iter = obstacle_y[y].begin(); iter != obstacle_y[y].end(); ++iter) {
                  if (*iter > x && *iter <= next_x) {  // 遇到障碍点
                    next_x = *iter - 1;
                    break;
                  }
                }
              }
              break;
            case 1:  // 向南 逆序遍历
              if (obstacle_x.count(x) != 0) {
                for (auto iter = obstacle_x[x].rbegin(); iter != obstacle_x[x].rend(); ++iter) {
                  if (*iter < y && *iter >= next_y) {  // 遇到障碍点
                    next_y = *iter + 1;
                    break;
                  }
                }
              }
              break;
            case 2:  // 向西 逆序遍历
              if (obstacle_y.count(y) != 0) {
                for (auto iter = obstacle_y[y].rbegin(); iter != obstacle_y[y].rend(); ++iter) {
                  if (*iter < x && *iter >= next_x) {  // 遇到障碍点
                    next_x = *iter + 1;
                    break;
                  }
                }
              }
              break;
            case 3:  // 向北 顺序遍历
              if (obstacle_x.count(x) != 0) {
                for (auto iter = obstacle_x[x].begin(); iter != obstacle_x[x].end(); ++iter) {
                  if (*iter > y && *iter <= next_y) {  // 遇到障碍点
                    next_y = *iter - 1;
                    break;
                  }
                }
              }
              break;
              break;
            default:
              break;
          }
          x = next_x;
          y = next_y;
          max_dist = max(max_dist, x * x + y * y);
          break;
      }
    }
    return max_dist;
  }
};

官方题解（修改后）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
using Coord = pair<int, int>;
struct CoordHash {
  size_t operator()(const Coord& c) const {
    auto fn = hash<int>();
    return fn(c.first) ^ fn(c.second);
  }
};
class Solution {
 public:
  int robotSim(vector<int>& commands, vector<vector<int>>& obstacles) {
    unordered_set<Coord, CoordHash> obstacle_set;
    for (auto& obstacle : obstacles) {  // 加入障碍点集合
      obstacle_set.emplace(Coord{obstacle[0], obstacle[1]});
    }
    int dir[4][2] = {{1, 0}, {0, -1}, {-1, 0}, {0, 1}};  // 东 南 西 北
    int index = 3;
    int x = 0;
    int y = 0;
    int max_dist = 0;
    int next_x;
    int next_y;
    for (int cmd : commands) {
      switch (cmd) {
        case -1:
          index = (index + 1) % 4;  // 右转90度
          break;
        case -2:
          index = (index + 3) % 4;  // 左转90度
          break;
        default:
          next_x = x + dir[index][0] * cmd;
          next_y = y + dir[index][1] * cmd;
          for (int k = 1; k <= cmd; k++) {
            if (obstacle_set.count({x + dir[index][0] * k, y + dir[index][1] * k}) != 0) {  // 遇见障碍，回退到前一个点
              next_x = x + dir[index][0] * (k - 1);
              next_y = y + dir[index][1] * (k - 1);
              break;
            }
          }
          x = next_x;
          y = next_y;
          max_dist = max(max_dist, x * x + y * y);
          break;
      }
    }
    return max_dist;
  }
};

我的解法比官方题解多很多代码的点在于没有很好利用dir[index][0]和dir[index][1]，而是对index进行分类（东南西北），另外想利用机器人走直线的特点，x全部相等或y全部相等，但遍历时不能直接跳转到出发点，仍需从头或从尾开始遍历，效率很低，不如直接一个一个坐标判断是否在障碍点集合中。
在 C++ 中用 lambda 函数自定义 unordered_set 时，为什么赋值运算符失效了？

从给定原材料中找到所有可以做出的菜

题目简要：
你有 n 道不同菜的信息。给你一个字符串数组 recipes 和一个二维字符串数组 ingredients 。第 i 道菜的名字为 recipes[i] ，如果你有它 所有 的原材料 ingredients[i] ，那么你可以 做出 这道菜。一道菜的原材料可能是 另一道 菜，也就是说 ingredients[i] 可能包含 recipes 中另一个字符串。
同时给你一个字符串数组 supplies ，它包含你初始时拥有的所有原材料，每一种原材料你都有无限多。
请你返回你可以做出的所有菜。你可以以 任意顺序 返回它们。
注意两道菜在它们的原材料中可能互相包含。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  vector<string> findAllRecipes(vector<string>& recipes, vector<vector<string>>& ingredients, vector<string>& supplies) {
    unordered_map<string, int> recipe_map;
    unordered_set<string> supply_set;
    int recipe_size = recipes.size();
    vector<vector<int>> adjacency_list(recipe_size);  // 邻接表
    vector<int> induity(recipe_size, 0);              // 入度矩阵
    vector<int> result(recipe_size, -1);              // -1 初始化 0 不能做 1 能做
    for (int i = 0; i < recipe_size; i++) {
      recipe_map[recipes[i]] = i;
    }
    for (string& supply : supplies) {
      supply_set.emplace(supply);
    }

    for (int i = 0; i < recipe_size; i++) {
      bool include_all_ingredient = true;
      for (string& ingredient : ingredients[i]) {
        if (supply_set.count(ingredient) == 0) {  // 不在原材料列表
          include_all_ingredient = false;
          auto iter = recipe_map.find(ingredient);
          if (iter == recipe_map.end()) {  // 不在菜单列表，不可能做出该菜
            induity[i] = 0;                // 将入度设为0
            result[i] = 0;
            break;
          } else {  // 配菜添加指向当前菜的边，入度加一
            adjacency_list[iter->second].emplace_back(i);
            induity[i]++;
          }
        }
      }
      if (include_all_ingredient) {  // 拥有所有原材料，可以做出来
        result[i] = 1;
      }
    }

    queue<int> in_queue;
    for (int i = 0; i < recipe_size; i++) {  // 将入度为0的节点压入队列
      if (induity[i] == 0) {
        in_queue.emplace(i);
      }
    }
    while (!in_queue.empty()) {
      int i = in_queue.front();
      in_queue.pop();
      for (int j : adjacency_list[i]) {
        induity[j]--;
        if (induity[j] == 0) {  // 若入度变为0，加入队列
          in_queue.emplace(j);
        }
        if (result[i] == 0) {  // 如果配菜不能做出来，这菜也不可能做出来
          result[j] = 0;
        } else if (result[j] != 0) {  // 如果配菜可以做出来
          result[j] = 1;
        }
      }
    }
    vector<string> ans;
    for (int i = 0; i < recipe_size; i++) {
      if (result[i] == 1 && induity[i] == 0) {  // 判断入度为0用来解决环问题
        ans.emplace_back(recipes[i]);
      }
    }
    return ans;
  }
};

最后再次判断入度以解决环问题
官方题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    vector<string> findAllRecipes(vector<string>& recipes, vector<vector<string>>& ingredients, vector<string>& supplies) {
        int n = recipes.size();
        // 图
        unordered_map<string, vector<string>> depend;
        // 入度统计
        unordered_map<string, int> cnt;
        for (int i = 0; i < n; ++i) {
            for (const string& ing: ingredients[i]) {
                depend[ing].push_back(recipes[i]);
            }
            cnt[recipes[i]] = ingredients[i].size();
        }
        
        vector<string> ans;
        queue<string> q;
        // 把初始的原材料放入队列
        for (const string& sup: supplies) {
            q.push(sup);
        }
        // 拓扑排序
        while (!q.empty()) {
            string cur = q.front();
            q.pop();
            if (depend.count(cur)) {
                for (const string& rec: depend[cur]) {
                    --cnt[rec];
                    // 如果入度变为 0，说明可以做出这道菜
                    if (cnt[rec] == 0) {
                        ans.push_back(rec);
                        q.push(rec);
                    }
                }
            }
        }
        return ans;
    }
};

评论：
学习了，用菜做菜肴，不要用菜肴找菜。

  • 有鸡蛋，可以用来做煎蛋，煮蛋，鸡蛋羹，鸡蛋布丁
  • 有煎蛋，可以拿来做三明治，汉堡，夹心煎饼

但是用菜肴找菜，就会存在套娃问题。

  • 我想要鸡蛋，需要先获得母鸡
  • 想要母鸡，需要先获得鸡蛋

翻转卡片游戏

题目简要：
在桌子上有 N 张卡片，每张卡片的正面和背面都写着一个正数（正面与背面上的数有可能不一样）。
我们可以先翻转任意张卡片，然后选择其中一张卡片。
如果选中的那张卡片背面的数字 X 与任意一张卡片的正面的数字都不同，那么这个数字是我们想要的数字。
哪个数是这些想要的数字中最小的数（找到这些数中的最小值）呢？如果没有一个数字符合要求的，输出 0。
其中, fronts[i] 和 backs[i] 分别代表第 i 张卡片的正面和背面的数字。
如果我们通过翻转卡片来交换正面与背面上的数，那么当初在正面的数就变成背面的数，背面的数就变成正面的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  int flipgame(vector<int>& fronts, vector<int>& backs) {
    const int n = fronts.size();
    map<int, int> number_map;
    for (int i = 0; i < n; i++) {
      if (fronts[i] == backs[i]) {  // 相同的正反牌
        number_map[fronts[i]] = n + 1;
      } else {
        number_map[fronts[i]]++;
        number_map[backs[i]]++;
      }
    }
    for (auto& kv : number_map) {  // map为红黑树实现，元素有序
      if (kv.second <= n) {        // 该数不存在相同的正反牌
        return kv.first;
      }
    }
    return 0;  // 未找到符合要求的数字
  }
};

多使用哈希表与集合，把它们当做树 图一样的解题数据结构

元音拼写检查器

题目简要
在给定单词列表 wordlist 的情况下，我们希望实现一个拼写检查器，将查询单词转换为正确的单词。
对于给定的查询单词 query，拼写检查器将会处理两类拼写错误：
大小写：如果查询匹配单词列表中的某个单词（不区分大小写），则返回的正确单词与单词列表中的大小写相同。
例如：wordlist = [“yellow”], query = “YellOw”: correct = “yellow”
例如：wordlist = [“Yellow”], query = “yellow”: correct = “Yellow”
例如：wordlist = [“yellow”], query = “yellow”: correct = “yellow”
元音错误：如果在将查询单词中的元音 (‘a’, ‘e’, ‘i’, ‘o’, ‘u’) 分别替换为任何元音后，能与单词列表中的单词匹配（不区分大小写），则返回的正确单词与单词列表中的匹配项大小写相同。
例如：wordlist = [“YellOw”], query = “yollow”: correct = “YellOw”
例如：wordlist = [“YellOw”], query = “yeellow”: correct = “” （无匹配项）
例如：wordlist = [“YellOw”], query = “yllw”: correct = “” （无匹配项）
此外，拼写检查器还按照以下优先级规则操作：

当查询完全匹配单词列表中的某个单词（区分大小写）时，应返回相同的单词。
当查询匹配到大小写问题的单词时，您应该返回单词列表中的第一个这样的匹配项。
当查询匹配到元音错误的单词时，您应该返回单词列表中的第一个这样的匹配项。
如果该查询在单词列表中没有匹配项，则应返回空字符串。
给出一些查询 queries，返回一个单词列表 answer，其中 answer[i] 是由查询 query = queries[i] 得到的正确单词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  string modifyError(const string& origin, bool vowel_option) {  // 修改错误，附带元音纠错选项
    int len = origin.length();
    string feature;
    feature.resize(len);
    const string vowel = "aeiouAEIOU";
    for (int i = 0; i < len; i++) {
      if (vowel_option && vowel.find(origin[i]) != string::npos) {  // 元音全部用'a'代表
        feature[i] = 'a';
      } else if (origin[i] <= 'Z') {  // 字母全部变成小写便于比较
        feature[i] = origin[i] + ('a' - 'A');
      } else {
        feature[i] = origin[i];
      }
    }
    return feature;
  }
  vector<string> spellchecker(vector<string>& wordlist, vector<string>& queries) {
    int word_size = wordlist.size();
    unordered_map<string, int> right_map;
    unordered_map<string, int> case_error_map;
    unordered_map<string, int> vowel_error_map;
    for (int i = word_size - 1; i >= 0; i--) {  // 逆序添加，保证相同的key最后的i最小
      right_map[wordlist[i]] = i;
      case_error_map[modifyError(wordlist[i], false)] = i;
      vowel_error_map[modifyError(wordlist[i], true)] = i;
    }
    vector<string> result;
    for (string& query : queries) {
      auto iter = right_map.find(query);  // 寻找完全匹配的单词
      if (iter != right_map.end()) {
        result.emplace_back(wordlist[iter->second]);
        continue;
      }
      iter = case_error_map.find(modifyError(query, false));  // 选择大小写错误的单词
      if (iter != case_error_map.end()) {
        result.emplace_back(wordlist[iter->second]);
        continue;
      }
      iter = vowel_error_map.find(modifyError(query, true));  // 寻找元音错误的单词
      if (iter != case_error_map.end()) {
        result.emplace_back(wordlist[iter->second]);
        continue;
      }
      result.emplace_back("");  // 未找到，加入空字符串
    }
    return result;
  }
};

使用map/set加速查找，用空间换时间
未使用map直接查找的版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  string modifyError(const string& origin, bool vowel_option) {
    int len = origin.length();
    string feature;
    feature.resize(len);
    const string vowel = "aeiouAEIOU";
    for (int i = 0; i < len; i++) {
      if (vowel_option && vowel.find(origin[i]) != string::npos) {
        feature[i] = 'a';
      } else if (origin[i] <= 'Z') {
        feature[i] = origin[i] + ('a' - 'A');
      } else {
        feature[i] = origin[i];
      }
    }
    return feature;
  }
  vector<string> spellchecker(vector<string>& wordlist, vector<string>& queries) {
    int word_size = wordlist.size();
    vector<string> case_error;
    vector<string> vowel_error;
    for (string& word : wordlist) {
      case_error.emplace_back(modifyError(word, false));
      vowel_error.emplace_back(modifyError(word, true));
    }
    vector<string> result;
    for (string& query : queries) {
      bool find = false;
      for (int i = 0; i < word_size; i++) {
        if (wordlist[i] == query) {
          result.emplace_back(wordlist[i]);
          find = true;
          break;
        }
      }
      if (find == false) {
        string case_query = modifyError(query, false);
        for (int i = 0; i < word_size; i++) {
          if (case_error[i] == case_query) {
            result.emplace_back(wordlist[i]);
            find = true;
            break;
          }
        }
      }
      if (find == false) {
        string vowel_query = modifyError(query, true);
        for (int i = 0; i < word_size; i++) {
          if (vowel_error[i] == vowel_query) {
            result.emplace_back(wordlist[i]);
            find = true;
            break;
          }
        }
      }
      if (find == false) {
        result.emplace_back("");
      }
    }
    return result;
  }
};

信物传送

题目简要：
本次试炼场地设有若干传送带，matrix[i][j] 表示第 i 行 j 列的传送带运作方向，”^”,”v”,”<”,”>” 这四种符号分别表示 上、下、左、右 四个方向。信物会随传送带的方向移动。勇者每一次施法操作，可临时变更一处传送带的方向，在物品经过后传送带恢复原方向。
结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
const int kInf = 0x7fffffff;
struct Node {
  Node() {}
  Node(int x, int y, int value) {
    this->x = x;
    this->y = y;
    this->value = value;
  }
  bool operator<(const Node& node) const { return this->value > node.value; }  // 距离越小优先级越高
  int x;
  int y;
  int value;
};
class Solution {
 public:
  bool check(int x, int y, int n, int m) {
    if (x >= 0 && x < n && y >= 0 && y < m) {
      return true;
    }
    return false;
  }
  int conveyorBelt(vector<string>& matrix, vector<int>& start, vector<int>& end) {
    int row = matrix.size();
    int col = matrix[0].size();
    vector<vector<int>> dist(row, vector<int>(col, kInf));
    vector<vector<bool>> marked(row, vector<bool>(col, false));
    priority_queue<Node> small_heap;
    // 注意坐标轴与箭头方向，坑！
    int dir[4][2] = {0, 1, 1, 0, 0, -1, -1, 0};
    map<char, int> symbol = {{'>', 0}, {'v', 1}, {'<', 2}, {'^', 3}};  // 箭头符号与dir数组索引
    dist[start[0]][start[1]] = 0;
    small_heap.emplace(Node{start[0], start[1], 0});  // 压入起始节点
    while (!small_heap.empty()) {
      auto node = small_heap.top();
      small_heap.pop();
      marked[node.x][node.y] = true;  // 加入结果集合
      if (node.x == end[0] && node.y == end[1]) {
        return node.value;
      }
      for (int i = 0; i < 4; i++) {  // 遍历四个方向
        int next_x = node.x + dir[i][0];
        int next_y = node.y + dir[i][1];
        if (check(next_x, next_y, row, col) && !marked[next_x][next_y]) {  // 如果节点合法且未加入结果集合
          if (i == symbol[matrix[node.x][node.y]]) {                       // 箭头指向的方向，两点距离为0
            dist[next_x][next_y] = min(dist[next_x][next_y], node.value);
          } else {  // 其他情况距离为1
            dist[next_x][next_y] = min(dist[next_x][next_y], node.value + 1);
          }
          small_heap.emplace(Node{next_x, next_y, dist[next_x][next_y]});
        }
      }
    }
    return dist[end[0]][end[1]];
  }
};

lambda表达式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const int kInf = 0x7fffffff;
using Node = tuple<int, int, int>;
class Solution {
 public:
  bool check(int x, int y, int n, int m) {
    if (x >= 0 && x < n && y >= 0 && y < m) {
      return true;
    }
    return false;
  }
  int conveyorBelt(vector<string>& matrix, vector<int>& start, vector<int>& end) {
    int row = matrix.size();
    int col = matrix[0].size();
    vector<vector<int>> dist(row, vector<int>(col, kInf));
    vector<vector<bool>> marked(row, vector<bool>(col, false));
    auto compare = [](const Node& node1, const Node& node2) -> bool { return get<0>(node1) > get<0>(node2); };  // 自定义比较函数
    priority_queue<Node, vector<Node>, decltype(compare)> small_heap(compare);
    // 注意坐标轴与箭头方向，坑！
    int dir[4][2] = {0, 1, 1, 0, 0, -1, -1, 0};
    map<char, int> symbol = {{'>', 0}, {'v', 1}, {'<', 2}, {'^', 3}};  // 箭头符号与dir数组索引
    dist[start[0]][start[1]] = 0;
    small_heap.emplace(Node{0, start[0], start[1]});  // 压入起始节点
    while (!small_heap.empty()) {
      auto [val, x, y] = small_heap.top();
      small_heap.pop();
      marked[x][y] = true;  // 加入结果集合
      if (x == end[0] && y == end[1]) {
        return val;
      }
      for (int i = 0; i < 4; i++) {  // 遍历四个方向
        int next_x = x + dir[i][0];
        int next_y = y + dir[i][1];
        if (check(next_x, next_y, row, col) && !marked[next_x][next_y]) {  // 如果节点合法且未加入结果集合
          if (i == symbol[matrix[x][y]]) {                                 // 箭头指向的方向，两点距离为0
            dist[next_x][next_y] = min(dist[next_x][next_y], val);
          } else {  // 其他情况距离为1
            dist[next_x][next_y] = min(dist[next_x][next_y], val + 1);
          }
          small_heap.emplace(Node{dist[next_x][next_y], next_x, next_y});
        }
      }
    }
    return dist[end[0]][end[1]];
  }
};

使用方向数组简化处理流程
c++优先队列priority_queue（自定义比较函数）
C++函数指针、函数对象与C++11 function对象对比分析
【C++深陷】之“decltype”

引爆最多的炸弹

题目简要:给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。
炸弹用一个下标从 0 开始的二维整数数组 bombs 表示，其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标，ri 表示爆炸范围的 半径 。
你需要选择引爆 一个 炸弹。当这个炸弹被引爆时，所有 在它爆炸范围内的炸弹都会被引爆，这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。
给你数组 bombs ，请你返回在引爆 一个 炸弹的前提下，最多 能引爆的炸弹数目。

邻接矩阵实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
 public:
  bool inRadius(vector<int> start, vector<int> end) {  // 判断两点是否在起点圆内
    ll dist = (ll)(start[0] - end[0]) * (start[0] - end[0]) + (ll)(start[1] - end[1]) * (start[1] - end[1]);
    return (ll)(start[2]) * start[2] >= dist;
  }
  int maximumDetonation(vector<vector<int>>& bombs) {
    int bomb_number = bombs.size();
    vector<vector<bool>> connected(bomb_number, vector<bool>(bomb_number));  // 各节点是否连通
    for (int i = 0; i < bomb_number; i++) {
      for (int j = 0; j < bomb_number; j++) {
        if (i != j) {  // 自己与自己相连
          connected[i][j] = inRadius(bombs[i], bombs[j]);
        }
      }
    }

    int visit_node;
    int visit_node_num;
    int max_visit_node_num = 1;
    queue<int> visit_queue;
    vector<bool> marked(bomb_number, false);  // 节点是否被访问过
    vector<int> trace(bomb_number, -1);       // 是否在一次遍历中被访问过，用于解决环的问题
    for (int i = 0; i < bomb_number; i++) {
      if (marked[i] == false) {
        trace[i] = i;  // 用起始节点号标识本次遍历
        visit_node_num = 0;
        visit_queue.emplace(i);  // 压入节点，开始一轮遍历

        while (!visit_queue.empty()) {
          visit_node = visit_queue.front();
          visit_queue.pop();

          marked[visit_node] = true;
          visit_node_num++;
          for (int j = 0; j < bomb_number; j++) {
            if (trace[j] != i && connected[visit_node][j] == true) {
              visit_queue.emplace(j);
              trace[j] = i;  // 在本次遍历中被访问
            }
          }
        }
        max_visit_node_num = max(max_visit_node_num, visit_node_num);
      }
    }
    return max_visit_node_num;
  }
};

邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
 public:
  bool inRadius(vector<int> start, vector<int> end) {  // 判断两点是否在起点圆内
    ll dist = (ll)(start[0] - end[0]) * (start[0] - end[0]) + (ll)(start[1] - end[1]) * (start[1] - end[1]);
    return (ll)(start[2]) * start[2] >= dist;
  }
  int maximumDetonation(vector<vector<int>>& bombs) {
    int bomb_number = bombs.size();
    vector<vector<int>> connected(bomb_number);  // 各节点是否连通
    for (int i = 0; i < bomb_number; i++) {
      for (int j = 0; j < bomb_number; j++) {
        if (i != j && inRadius(bombs[i], bombs[j])) {
          connected[i].emplace_back(j);
        }
      }
    }
    queue<int> visit_queue;
    int visit_node;
    int visit_node_num;
    int max_visit_node_num = 1;
    vector<bool> marked(bomb_number, false);  // 节点是否被访问过
    vector<int> trace(bomb_number, -1);       // 是否在一次遍历中被访问过，用于解决环的问题
    for (int i = 0; i < bomb_number; i++) {
      if (marked[i] == false) {
        trace[i] = i;  // 用起始节点号标识本次遍历
        visit_node_num = 0;
        visit_queue.emplace(i);  // 压入该节点，开始遍历
        while (!visit_queue.empty()) {
          visit_node = visit_queue.front();
          visit_queue.pop();

          marked[visit_node] = true;
          visit_node_num++;
          for (int j : connected[visit_node]) {
            if (trace[j] != i) {
              visit_queue.emplace(j);
              trace[j] = i;
            }
          }
        }
        max_visit_node_num = max(max_visit_node_num, visit_node_num);
      }
    }
    return max_visit_node_num;
  }
};

使用trace避免环问题，使用marked去除没必要的节点遍历

从二叉树一个节点到另一个节点每一步的方向

题目简要：
给你一棵 二叉树 的根节点 root ，这棵二叉树总共有 n 个节点。每个节点的值为 1 到 n 中的一个整数，且互不相同。给你一个整数 startValue ，表示起点节点 s 的值，和另一个不同的整数 destValue ，表示终点节点 t 的值。
请找到从节点 s 到节点 t 的 最短路径 ，并以字符串的形式返回每一步的方向。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
 public:
  bool findValue(TreeNode *node, int target_value, vector<int> &trace) {
    if (node->val == target_value) {  // 找到目标值
      return true;
    }
    if (node->left != nullptr) {
      if (findValue(node->left, target_value, trace)) {  // 左子树找到目标，将-1（左）加入轨迹
        trace.emplace_back(-1);
        return true;
      }
    }
    if (node->right != nullptr) {
      if (findValue(node->right, target_value, trace)) {  // 右子树找到目标，将1（右）加入轨迹
        trace.emplace_back(1);
        return true;
      }
    }
    return false;
  }
  string getDirections(TreeNode *root, int startValue, int destValue) {
    vector<int> trace1, trace2;
    findValue(root, startValue, trace1);  // 获取根节点到起始节点的逆序轨迹
    findValue(root, destValue, trace2);   // 获取根节点到终止节点的逆序轨迹
    int i = trace1.size() - 1;
    int j = trace2.size() - 1;
    while (i >= 0 && j >= 0 && trace1[i] == trace2[j]) {  // 去掉末尾共同的轨迹，找到共同的父节点
      i--;
      j--;
    }
    string ans = string(i + 1, 'U');  // 起始节点需一直前往父节点，直到共同的父节点
    while (j >= 0) {                  // 从共同父节点到终止节点的轨迹
      if (trace2[j] == 1) {
        ans.push_back('R');
      } else {
        ans.push_back('L');
      }
      j--;
    }
    return ans;
  }
};

回溯法得到逆序轨迹
递归第一要义：相信自己已经写出了递归函数，然后进行调用。

最长回文子串

使用备忘录的递归方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
const int kNotInitialized = -1;
class Solution {
 public:
  string longestPalindrome(string s) {
    int len = s.length();
    memo = vector<vector<int>>(len, vector<int>(len, kNotInitialized));  // 初始化备忘录
    for (int j = len; j >= 1; j--) {                                     // 回文串长度为主序
      for (int i = 0; i < len - j + 1; i++) {                            // 改变起始索引
        if (isPalindrome(s, i, i + j - 1)) {
          return s.substr(i, j);
        }
      }
    }
    return "";
  }
  bool isPalindrome(string& s, int i, int j) {
    if (memo[i][j] != kNotInitialized) {  // 如果存在记录，直接返回
      return memo[i][j] == 1;
    }
    if (i >= j) {  // 奇数回文字符串i j相等终止，偶数回文字符串交错时相等
      memo[i][j] = 1;
      return true;
    }
    if (s[i] == s[j]) {
      memo[i][j] = isPalindrome(s, i + 1, j - 1) ? 1 : 0;  // 两边字符相等，判断内侧字符串是否为回文字符串
      return memo[i][j] == 1;
    } else {
      memo[i][j] = 0;
      return false;
    }
  }

 private:
  vector<vector<int>> memo;
};

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
 public:
  string longestPalindrome(string s) {
    int len = s.length();
    vector<vector<int>> dp(len, vector<int>(len));  // 初始化DPtable
    for (int i = 0; i < len - 1; i++) {             // 一个字符一定为回文字符串
      dp[i][i] = 1;
    }
    int longest_palindrome_length = 1;
    int longest_palindrome_start = 0;
    int end;
    for (int palindrome_length = 2; palindrome_length <= len; palindrome_length++) {  // 回文字符串长度从小到大
      for (int start = 0; start < len - palindrome_length + 1; start++) {             // 改变起始位置
        end = start + palindrome_length - 1;                                          // 字符串末尾位置
        if (s[start] == s[end]) {
          if (end - start < 3) {  // 中间隔一个字符或相邻
            dp[start][end] = 1;
          } else {
            dp[start][end] = dp[start + 1][end - 1];  // 取决于内侧字符串是否为回文字符串
          }
        } else {
          dp[start][end] = 0;
        }
        if (dp[start][end] == 1 && palindrome_length > longest_palindrome_length) {  // 更新最大回文字符串长度与起始位置
          longest_palindrome_length = palindrome_length;
          longest_palindrome_start = start;
        }
      }
    }
    return s.substr(longest_palindrome_start, longest_palindrome_length);
  }
};

1.递归方法自顶向下，动态规划自底向上
2.递归方法时回文串长度从大到小，保证第一时间找到最大回文字符串
3.动态规划方法时回文串长度从小到大，保证内侧字符串结果已产生(dp[i+1][j-1]）

只出现一次的数字

只出现一次的数字
题目简要：给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans =0;
        for(int num:nums){
            ans ^= num;
        }
        return ans;
    }
};

异或运算性质

其他数字出现三次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
 public:
  int singleNumber(vector<int>& nums) {
    int ans = 0;
    int bit_num = 0;
    for (int i = 0; i < 32; i++) {  // 0-31位
      bit_num = 0;
      for (int num : nums) {
        bit_num += (num >> i & 1);  // 取数字的第i位
      }
      if (bit_num % 3 != 0) {  // 答案数字该位为1
        ans |= 1 << i;
      }
    }
    return ans;
  }
};

位运算

二叉搜索树中两个节点之和

剑指 Offer II 056. 二叉搜索树中两个节点之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
 public:
  void preOrderTraversal(TreeNode *node, vector<int> &sort_list) {  // 中序遍历得到有序序列
    if (node == nullptr) {                                          //  节点为空，直接返回
      return;
    }
    preOrderTraversal(node->left, sort_list);   // 先访问左子树
    sort_list.emplace_back(node->val);          // 再访问根节点
    preOrderTraversal(node->right, sort_list);  // 最后访问右子树
  }
  bool findTarget(TreeNode *root, int k) {
    vector<int> sort_list;
    preOrderTraversal(root, sort_list);
    // 头尾两个指针
    int p = 0;
    int q = sort_list.size() - 1;
    int sum;
    while (p < q) {
      sum = sort_list[p] + sort_list[q];
      if (sum > k) {  // 数字过大，末尾指针前移
        q--;
      } else if (sum < k) {  // 数字过小，头部指针后移
        p++;
      } else {  // 找到相应数字，返回结果
        return true;
      }
    }
    return false;
  }
};

中序遍历+双指针

多次求和构造目标数组

多次求和构造目标数组

给你一个整数数组 target 。一开始，你有一个数组 A ，它的所有元素均为 1 ，你可以执行以下操作：
令 x 为你数组里所有元素的和
选择满足 0 <= i < target.size 的任意下标 i ，并让 A 数组里下标为 i 处的值为 x 。
你可以重复该过程任意次
如果能从 A 开始构造出目标数组 target ，请你返回 True ，否则返回 False 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution {
 public:
  bool isPossible(vector<int>& target) {
    if (target.size() == 1) {  // 只有一个元素时，仅当该元素为1时正确
      return target[0] == 1;
    }

    ll sum = 0, other_number_sum = 0;
    priority_queue<int> max_queue;
    int max_value, divisor_number;
    for (int n : target) {  // 将所有元素压入优先队列并计算总和
      sum += n;
      max_queue.emplace(n);
    }

    while (true) {
      max_value = max_queue.top();
      max_queue.pop();
      other_number_sum = sum - max_value;             // 其他所有数的总和
      if (max_value == 1 || other_number_sum == 1) {  // 总能迭代至[1,1,1]的情况
        return true;
      }
      if (max_value <= other_number_sum || max_value % other_number_sum == 0) {  // 无法通过减other_number_sum迭代至[1,1,1]
        return false;
      }
      divisor_number = max_value / other_number_sum * other_number_sum;  // 减小到other_sum之下
      max_value -= divisor_number;
      sum -= divisor_number;
      max_queue.emplace(max_value);  // 重新加入优先队列
    }
    return false;
  }
};

解题关键：
1 最大值减去多个其余数之和而不是每次减去一个，提高程序执行效率
2 溢出情况，数组总和大于int最大值，其余数之和同样大于int最大值

全排列

题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
 public:
  void backtrack(const vector<int>& nums, vector<vector<int>>& res, vector<int>& output, vector<bool>& mark, int first, int len) {
    if (first == len) {
      res.emplace_back(output);
      return;
    }

    for (int i = 0; i < len; i++) {
      if (!mark[i]) {
        mark[i] = true;
        output.emplace_back(nums[i]);
        backtrack(nums, res, output, mark, first + 1, len);
        mark[i] = false;
        output.pop_back();
      }
    }
  }
  vector<vector<int>> permute(vector<int>& nums) {      // 借助标记数组，使用回溯法找到所有全排列
    int n = static_cast<int>(nums.size());
    vector<vector<int>> res;
    vector<bool> mark(n, false);
    vector<int> output;
    backtrack(nums, res, output, mark, 0, n);       
    return res;
  }
};

官方题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
 public:
  void backtrack(vector<int>& nums, vector<vector<int>>& res, int first, int len) {
    if (first == len) {
      res.emplace_back(nums);
      return;
    }

    for (int i = first; i < len; i++) {  // [0,first−1] 是已填过的数的集合，[first,n−1] 是待填的数的集合
      swap(nums[i], nums[first]);
      backtrack(nums, res, first + 1, len);
      swap(nums[i], nums[first]);
    }
  }
  vector<vector<int>> permute(vector<int>& nums) {  // 不使用标记数组
    int n = static_cast<int>(nums.size());
    vector<vector<int>> res;
    backtrack(nums, res, 0, n);
    return res;
  }
};

电话号码的字母组合

题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
 public:
  void traverse(const vector<string>& source, string combine, int start, int end, vector<string>& res) {
    if (start == end) {  // 到达末尾，加入结果集
      res.emplace_back(combine);
      return;
    }
    for (auto letter : source[start]) {  // 依次使用各个字母
      traverse(source, combine + letter, start + 1, end, res);
    }
  }
  vector<string> letterCombinations(string digits) {
    if (digits.empty()) {
      return {};
    }
    static vector<string> dig2str = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};  // 数字字母映射
    vector<string> strs;
    int idx;
    for (auto digit : digits) {  // 将数字转换成字母集合
      idx = static_cast<int>(digit - '2');
      strs.emplace_back(dig2str[idx]);
    }
    vector<string> res;
    int digit_len = static_cast<int>(digits.size());
    traverse(strs, "", 0, digit_len, res);  // 遍历
    return res;
  }
};

两个列表的最小索引总和

题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
 public:
  // 使用数组遍历的方式找到最小索引和的餐厅
  vector<string> findRestaurant(vector<string>& list1, vector<string>& list2) {
    int len1 = static_cast<int>(list1.size());
    int len2 = static_cast<int>(list2.size());
    int max_idx_sum = len1 + len2 - 2;
    bool flag = false;
    int low_bound;
    int high_bound;
    vector<string> res;
    for (int k = 0; k <= max_idx_sum; k++) {  // k为索引和
      low_bound = max(0, k + 1 - len2);
      high_bound = min(k, len1 - 1);
      for (int i = low_bound; i <= high_bound; i++) {
        if (list1[i] == list2[k - i]) {
          res.emplace_back(list1[i]);
          flag = true;
        }
      }
      if (flag) {
        break;
      }
    }
    return res;
  }
  // 官方题解，采用哈希表
  vector<string> findRestaurant(vector<string>& list1, vector<string>& list2) {
    int len1 = static_cast<int>(list1.size());
    int len2 = static_cast<int>(list2.size());
    unordered_map<string, int> index;
    for (int i = 0; i < len1; i++) {  // 插入字符串-索引对
      index.insert({list1[i], i});
    }

    int min_index_sum = len1 + len2 + 1;
    int index_sum;
    vector<string> res;
    for (int i = 0; i < len2; i++) {
      if (index.count(list2[i]) > 0) {  // 若存在相同餐厅名
        index_sum = index[list2[i]] + i;
        if (index_sum < min_index_sum) {
          res.clear();
          res.emplace_back(list2[i]);
          min_index_sum = index_sum;
        } else if (index_sum == min_index_sum) {
          res.emplace_back(list2[i]);
        }
      }
      if (i > min_index_sum) {  // 当前索引已经超过了最小索引和，直接退出循环，
        break;
      }
    }
    return res;
  }
};

IP 地址无效化

题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
 public:
  string defangIPaddr(string address) {
    string new_address;
    size_t last_pos = 0;
    size_t cur_pos;
    while ((cur_pos = address.find('.', last_pos)) != address.npos) {
      new_address.append(address, last_pos, cur_pos - last_pos);  // 将两.之间的字符添加至字符串
      new_address.append("[.]");                                  // 插入[.]
      last_pos = cur_pos + 1;                                     // 更新last_pos，+1跳过字符'.'
    }
    new_address.append(address, last_pos, address.length() - last_pos);  // 添加末尾字符串
    return new_address;
  }
};

一个图中连通三元组的最小度数

题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
 public:
  const int kInf = 0x7fffffff;
  // 直接枚举
  int minTrioDegree(int n, vector<vector<int>>& edges) {
    vector<vector<int>> matrix(n + 1, vector<int>(n + 1, 0));
    vector<int> degree(n + 1, 0);
    for (auto edge : edges) {  // 构建邻接表
      matrix[edge[0]][edge[1]] = 1;
      matrix[edge[1]][edge[0]] = 1;
      degree[edge[0]]++;  // 计算各节点的度
      degree[edge[1]]++;
    }
    int min_degree = kInf;
    int triple_degree;
    for (int i = 1; i <= n - 2; i++) {
      if (min_degree == 0) {  // 最小度为0，直接返回
        break;
      }
      for (int j = i + 1; j <= n - 1; j++) {
        if (matrix[i][j] == 1) {  // 如果i j之间存在边
          for (int k = j + 1; k <= n; k++) {
            if (matrix[i][k] == 1 && matrix[j][k] == 1) {  // 存在共同边
              triple_degree = degree[i] + degree[j] + degree[k] - 6;
              min_degree = min(min_degree, triple_degree);
            }
          }
        }
      }
    }
    if (min_degree == kInf) {
      return -1;
    }
    return min_degree;
  }
};

最短公共超序列

题目链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
 public:
  string shortestCommonSupersequence(string str1, string str2) {
    int m = static_cast<int>(str1.size());
    int n = static_cast<int>(str2.size());
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (int i = 1; i <= m; i++) {  // 由状态转移方程求dp数组
      for (int j = 1; j <= n; j++) {
        if (str1[i - 1] == str2[j - 1]) {
          dp[i][j] = dp[i - 1][j - 1] + 1;
        } else {
          dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
        }
      }
    }
    int i = m;
    int j = n;
    string lcs;
    while (i >= 1 && j >= 1) {  // 倒推出最长公共子序列
      if (str1[i - 1] == str2[j - 1]) {
        lcs.push_back(str1[i - 1]);
        i--;
        j--;
      } else {
        if (dp[i - 1][j] > dp[i][j - 1]) {  // 未选择str1
          i--;
        } else {  // 未选择str2
          j--;
        }
      }
    }
    i = 0;
    j = 0;
    string ans;
    for (auto iter = lcs.rbegin(); iter != lcs.rend(); iter++) {  // 填充字符
      while (i < m && str1[i] != *iter) {                         // 不在公共子序列中
        ans.push_back(str1[i]);
        i++;
      }
      while (j < n && str2[j] != *iter) {  // 不在公共子序列中
        ans.push_back(str2[j]);
        j++;
      }
      ans.push_back(*iter);  // 公共序列，只需填一次
      i++;
      j++;
    }
    // 处理剩余字符
    while (i < m) {
      ans.push_back(str1[i]);
      i++;
    }
    while (j < n) {
      ans.push_back(str2[j]);
      j++;
    }
    return ans;
  }
};

对照题解简单打一下，加深印象

有效的括号字符串

题目简要
给定一个只包含三种字符的字符串：（ ，） 和 *，写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则：
任何左括号 ( 必须有相应的右括号 )。
任何右括号 ) 必须有相应的左括号 ( 。
左括号 ( 必须在对应的右括号之前 )。
* 可以被视为单个右括号 ) ，或单个左括号 ( ，或一个空字符串。
一个空字符串也被视为有效字符串。

回溯+剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  // find_result: 是否找到合法表达式 bracket_diff：左括号数-右括号数 wildcard_num：当前通配符数目
  void backtrace(const string& s, int left_bracket_number, int start, bool& find_result, int bracket_diff, int wildcard_num) {
    if (find_result || left_bracket_number < 0 || abs(bracket_diff) > wildcard_num) {  // 提前结束：1 已找到合法表达式 2 表达式不合法 3 通配符无法满足需求
      return;
    }
    if (start == s.length()) {
      if (left_bracket_number == 0) {  // 表达式合法
        find_result = true;
      }
      return;
    }

    switch (s[start]) {
      case '(':
        backtrace(s, left_bracket_number + 1, start + 1, find_result, bracket_diff, wildcard_num);
        break;
      case ')':
        backtrace(s, left_bracket_number - 1, start + 1, find_result, bracket_diff, wildcard_num);
        break;
      case '*':
        backtrace(s, left_bracket_number + 1, start + 1, find_result, bracket_diff + 1, wildcard_num - 1);  // 替换为左括号
        backtrace(s, left_bracket_number, start + 1, find_result, bracket_diff, wildcard_num - 1);          // 替换为空字符串
        backtrace(s, left_bracket_number - 1, start + 1, find_result, bracket_diff - 1, wildcard_num - 1);  // 替换为右括号
        break;
      default:
        break;
    }
  }
  bool checkValidString(string s) {
    bool res = false;
    int wildcard_num = 0;   // 通配符数目
    int left_bracket = 0;   // 左括号数目
    int right_bracket = 0;  // 右括号数目
    for (char c : s) {      // 统计各符号数目
      switch (c) {
        case '(':
          left_bracket++;
          break;
        case ')':
          right_bracket++;
          break;
        case '*':
          wildcard_num++;
          break;
      }
    }
    backtrace(s, 0, 0, res, left_bracket - right_bracket, wildcard_num);
    return res;
  }
};

无法通过最后一个测试用例，超时

1
"*************************************************************************************************((*"

这是因为该样例太多通配符，且无法找到合法表达式，故可能情况接近3的100次方。
存在性问题若最终答案为不存在需穷举所有情况
官方动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  bool checkValidString(string s) {
    int len = s.length();
    vector<vector<bool>> dp(len, vector<bool>(len, false));  // dp[i][j]表示[i,j]子串是否合法
    for (int i = 0; i < len; i++) {                          // 长度为1的子串
      if (s[i] == '*') {
        dp[i][i] = true;
      }
    }
    for (int k = 2; k <= len; k++) {                                         // 子串长度
      for (int i = 0; i <= len - k; i++) {                                   // 起始索引
        int j = i + k - 1;                                                   // 子串末尾索引
        if ((s[i] == '(' || s[i] == '*') && (s[j] == ')' || s[j] == '*')) {  // 两端字符要求
          if (k == 2) {
            dp[i][j] = true;
          } else {
            dp[i][j] = dp[i + 1][j - 1];
          }
        }
        for (int x = i; x < j && dp[i][j] == false; x++) {  // 由两个子串拼接而成的表达式
          dp[i][j] = dp[i][x] && dp[x + 1][j];
        }
      }
    }
    return dp[0][len - 1];
  }
};

效率也低，但无所谓，只是用来熟悉动态规划的。

每个小孩最多能分到多少糖果

每个小孩最多能分到多少糖果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
 public:
  // 关键性质：如果能满足i，则一定能满足[0,i]区间任意数目
  int maximumCandies(vector<int>& candies, long long k) {
    auto check = [&](int i) -> bool {  // 判断k 个小孩能否按要求拿到 i 个糖果
      long long sum = 0;
      for (int candy : candies) {
        sum += candy / i;
      }
      return sum >= k;
    };
    // 计算无法达到需求的最小i
    int low = 1;
    int high = *max_element(candies.begin(), candies.end()) + 1;
    int mid;
    while (low < high) {
      mid = (low + high) / 2;
      if (check(mid)) {
        low = mid + 1;  // mid达到要求，+1
      } else {
        high = mid;
      }
    }
    // low-1即为最大糖果数目
    return low - 1;
  }
};

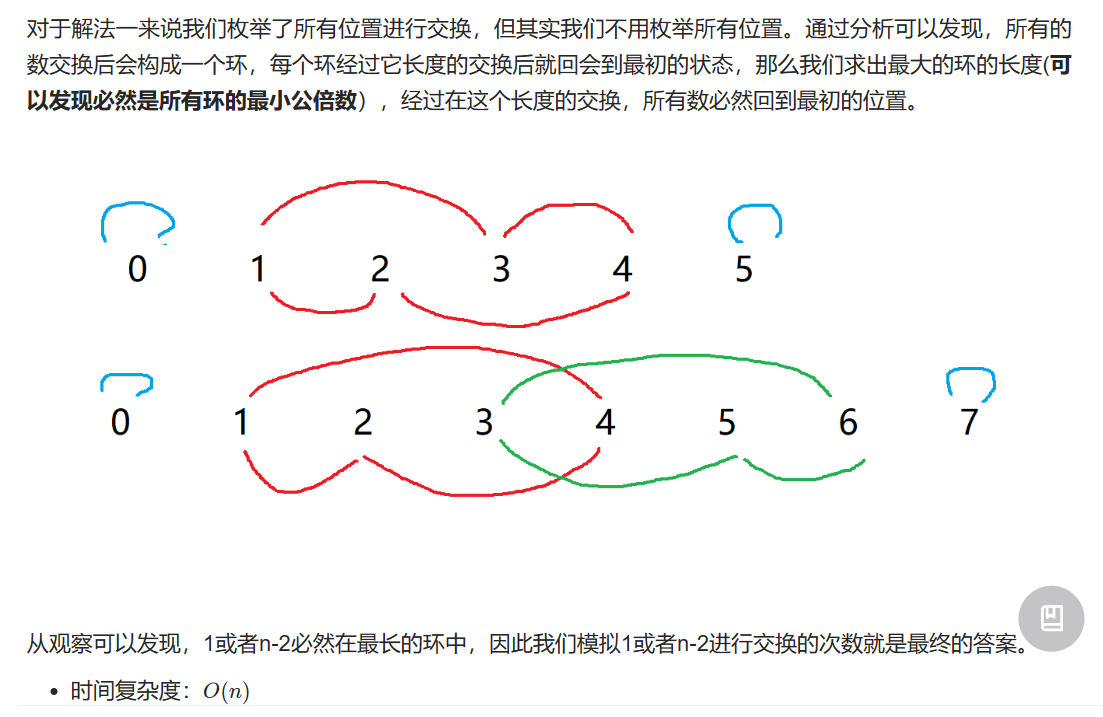
不是所有题目都是动态规划。

最大平均值和的分组

最大平均值和的分组

最优子结构：dp(i,j)由多个子问题的解dp(x,j-1)合成而来
无后效性：一旦dp(i,j)确定，就不再关心由哪个dp(x,j-1)得来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
using namespace std;

class Solution {
 public:
  double largestSumOfAverages(vector<int> &nums, int k) {
    int size = nums.size();
    if (size <= k) {  // 各个数为一个子数组
      double ans = 0;
      for (int num : nums) {
        ans += num;
      }
      return ans;
    }
    vector<double> prefix(size + 1);  // prefix[i]= nums[0]+nums[1]+...nums[i-1]
    prefix[0] = 0;
    for (int i = 1; i <= size; i++) {
      prefix[i] = prefix[i - 1] + nums[i - 1];
    }
    vector<vector<double>> dp(size + 1, vector<double>(k + 1));  // dp[i][j]：只有前i个数分成j个子数组的最大平均值
    for (int i = 1; i <= size; i++) {                            // j=1，即为整个数组平均值
      dp[i][1] = prefix[i] / i;
    }
    for (int j = 2; j <= k; j++) {
      for (int i = j; i <= size; i++) {
        // 计算dp[i][j]，此时i>=j，保证能分成j个子数组
        for (int x = j - 1; x < i; x++) {  //  j-1=< x <i 保证前面至少能分成j-1个子数组，后面能分一个子数组
          dp[i][j] = max(dp[i][j], dp[x][j - 1] + (prefix[i] - prefix[x]) / (i - x));
        }
      }
    }
    return dp[size][k];
  }

  double simple(vector<int> &nums, int k) {
    int size = nums.size();
    if (size <= k) {  
      double ans = 0;
      for (int num : nums) {
        ans += num;
      }
      return ans;
    }
    vector<double> prefix(size + 1);  
    prefix[0] = 0;
    for (int i = 1; i <= size; i++) {
      prefix[i] = prefix[i - 1] + nums[i - 1];
    }
    vector<double> dp(size + 1);      
    for (int i = 1; i <= size; i++) {  
      dp[i] = prefix[i] / i;
    }
    for (int j = 2; j <= k; j++) {
      for (int i = size; i >= j; i--) {  // 逆序保证dp[1] ... dp[i-1]为上一次计算的结果，即dp[1][j-1]...dp[i-1][j-1]
        for (int x = j - 1; x < i; x++) {  
          dp[i] = max(dp[i], dp[x] + (prefix[i] - prefix[x]) / (i - x));
        }
      }
    }
    return dp[size];
  }
};

动态规划有可能与前面任意一位有关，不一定是n-1位

牛客网

【2021】阿里巴巴编程题（2星）

【2021】阿里巴巴编程题（2星）

第一题 完美对


数组各数减去第一个数，归并相同特征的数组，使用map记录各数组的出现次数，对每一个map kv，查看map中是否存在相反数组，需对全0数组（相反数组为自身）进行特殊处理，为了避免重复计算，将相反数组出现次数置为-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
using namespace std;

vector<int> Another(const vector<int>& v) {
  vector<int> another(v.size());
  for (int i = 0; i < v.size(); i++) {
    another[i] = -v[i];
  }
  return another;
}
int main() {
  int n, k;
  while (cin >> n >> k) {
    vector<vector<int>> arr(n, vector<int>(k));
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < k; j++) {
        cin >> arr[i][j];
      }
    }
    map<vector<int>, int> ma;
    for (int i = 0; i < n; i++) {
      for (int j = k - 1; j >= 0; j--) {
        arr[i][j] -= arr[i][0];
      }
      ma[arr[i]]++;
    }
    int ans = 0;
    for (auto iter = ma.begin(); iter != ma.end(); ++iter) {
      if (iter->second == -1) {  // 标记为删除，跳过
        continue;
      }
      auto another_iter = ma.find(Another(iter->first));  // 寻找是否存在相反数组
      if (another_iter == iter) {                         // 全零数组，相反即本身
        ans += iter->second * (iter->second - 1) / 2;
      } else if (another_iter != ma.end()) {  // 后面存在相反数组
        ans += iter->second * another_iter->second;
        another_iter->second = -1;  // 标记为删除
      }
    }
    cout << ans << endl;
  }
}

第二题 选择物品


全排列变形问题，长度为m时输出结果，数字交换时强制要求序列递增，去重处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;

void dfs(vector<int>& vec, int start, int m) {
  if (start == m) {  // 长度达到要求，输出结果
    for (int i = 0; i < m; i++) {
      cout << vec[i] << " ";
    }
    cout << endl;
  } else {
    for (int i = start; i < vec.size(); i++) {
      if (start == 0 || vec[i] > vec[start - 1]) {  // 限制序列必须递增，去重
        swap(vec[i], vec[start]);
        dfs(vec, start + 1, m);
        swap(vec[i], vec[start]);
      }
    }
  }
}
int main() {
  int n, m;
  while (cin >> n >> m) {
    vector<int> arr(n);
    for (int i = 0; i < n; i++) {  // 初始化数组内容
      arr[i] = i + 1;
    }
    dfs(arr, 0, m);
  }
}

第三题 小强去春游


动态规划问题，假设已解决n-1与n-2规模时最短时间，可能的方法是：n-1 （最轻的人单独过河把最重的人接过来 fn-1+v0+vn） n-2（最轻的人过去 最重的和第二重的人过去 第二轻的人过来 第一第二轻的人过去 fn-2+v1+vn+v2+v2）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
#include <new>
using namespace std;

int main() {
  int T, n;
  cin >> T;
  for (int i = 0; i < T; i++) {
    cin >> n;
    vector<int> vec(n);
    for (int j = 0; j < n; j++) {
      cin >> vec[j];
    }
    sort(vec.begin(), vec.end());
    if (n == 1) {
      cout << vec[0] << endl;
      continue;
    }
    if (n == 2) {
      cout << vec[1] << endl;
      continue;
    }
    // 使用三个变量维持前两个 前一个 当前元素
    int first = vec[0];
    int second = vec[1];
    int three;
    for (int i = 2; i < n; i++) {
      // 状态转移方程
      three = min(second + vec[0] + vec[i], first + vec[i] + vec[0] + vec[1] * 2);
      // 更新序列
      first = second;
      second = three;
    }
    cout << three << endl;
  }
}

第四题 比例问题


枚举即可，时刻注意溢出问题，机试多使用long long

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
using namespace std;

int main() {
  long long A, B, a, b;  // 使用long long存储数字，防止溢出
  while (cin >> A >> B >> a >> b) {
    if (A > B * a / b) {  // 缩小查找范围
      A = B * a / b;
    }
    bool find = false;
    for (long long i = A; i >= 1; i--) {  // 逆序遍历可能数字
      if ((i * b) % a == 0) {
        cout << i << " " << i * b / a << endl;
        find = true;
        break;
      }
    }
    if (!find) {  // 不存在可能数字组合
      cout << 0 << " " << 0 << endl;
    }
  }
}

第五题 小强修水渠


最开始发现最小距离点一定在端点上（若有多个点，一定存在端点），故从前往后变量，计算端点的距离和，left为与左边点的长度和，right为与右边点的长度和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  while (cin >> n) {
    int x, y;
    vector<long long> vec(n);
    for (int i = 0; i < n; i++) {
      cin >> x >> y;
      vec[i] = x;
    }
    sort(vec.begin(), vec.end());
    long long left = 0; // 与左部端点的距离和
    long long right = accumulate(vec.begin(), vec.end(), -n * vec[0]); // 与右部端点的距离和
    long long min_len = left + right;
    for (int i = 1; i < n; i++) {
      left += i * (vec[i] - vec[i - 1]);
      right -= (n - i) * (vec[i] - vec[i - 1]);
      min_len = min(min_len, left + right);
    }
    cout << min_len << endl;
  }
}

后面发现最小距离和是中位数的性质，直接求中位数即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  while (cin >> n) {
    int x, y;
    vector<long long> vec(n);
    for (int i = 0; i < n; i++) {
      cin >> x >> y;
      vec[i] = x;
    }
    sort(vec.begin(), vec.end());
    long long x = (vec[n / 2] + vec[(n - 1) / 2]) / 2;	// 中位数
    int sum_len = 0;
    for (int xi : vec) {
      sum_len += abs(x - xi);
    }
    cout << sum_len << endl;
  }
}

第六题 国际交流会

最近小强主办了一场国际交流会，大家在会上以一个圆桌围坐在一起。由于大会的目的就是让不同国家的人感受一下不同的异域气息，为了更好地达到这个目的，小强希望最大化邻座两人之间的差异程度和。为此，他找到了你，希望你能给他安排一下座位，达到邻座之间的差异之和最大。

输入总共两行。
第一行一个正整数，代表参加国际交流会的人数(即圆桌上所坐的总人数，不单独对牛牛进行区分）
第二行包含个正整数，第个正整数a_i代表第个人的特征值。
其中
注意：
邻座的定义为: 第人的邻座为，第人的邻座是，第人的邻座是。
邻座的差异值计算方法为。
每对邻座差异值只计算一次。
输出总共两行。
第一行输出最大的差异值。
第二行输出用空格隔开的个数，为重新排列过的特征值。
（注意：不输出编号）
如果最大差异值情况下有多组解，输出任意一组即可。

思路
依次选取较大值与较小值即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  while (cin >> n) {
    vector<int> nums(n);
    for (int i = 0; i < n; i++) {
      cin >> nums[i];
    }
    sort(nums.begin(), nums.end());  // 数组排序
    vector<int> ans(n);
    for (int i = 0; i < n / 2; i++) {  // 依次选取较大值与较小值
      ans[2 * i] = nums[i];
      ans[2 * i + 1] = nums[n - i - 1];
    }
    ans[n - 1] = nums[n / 2];  // 奇数时最后一位未赋值
    long long diff = 0;        // 差异和
    for (int i = 0; i < n; i++) {
      diff += abs(ans[i] - ans[(i + 1) % n]);
    }
    cout << diff << endl;
    for (int num : ans) {
      cout << num << " ";
    }
    cout << endl;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  while (cin >> n) {
    vector<int> nums(n);
    for (int i = 0; i < n; i++) {
      cin >> nums[i];
    }
    sort(nums.begin(), nums.end());  // 数组排序
    vector<int> ans(n);
    // 双指针方式
    int low = 0;
    int high = n - 1;
    for (int i = 0; i < n; i++) {
      if (i % 2 == 0) {
        ans[i] = nums[low];
        low++;
      } else {
        ans[i] = nums[high];
        high--;
      }
    }
    long long diff = 0;  // 差异和
    for (int i = 0; i < n; i++) {
      diff += abs(ans[i] - ans[(i + 1) % n]);
    }
    cout << diff << endl;
    for (int num : ans) {
      cout << num << " ";
    }
    cout << endl;
  }
}

2021】阿里巴巴编程题（4星）

2021】阿里巴巴编程题（4星）

第一题 子集


经典的二维最长递增子序列问题，刚开始使用动态规划实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;

int main() {
  int T;
  cin >> T;
  for (int k = 0; k < T; k++) {
    int n, x, y;
    cin >> n;
    vector<pair<int, int>> item(n);
    for (int i = 0; i < n; i++) {
      cin >> item[i].first;
    }
    for (int i = 0; i < n; i++) {
      cin >> item[i].second;
    }
    auto cmp = [](const pair<int, int>& p1, const pair<int, int>& p2) -> bool { return p1.first < p2.first || (p1.first == p2.first && p1.second > p2.second); };
    sort(item.begin(), item.end(), cmp);  // 使用自定义排序函数
    vector<int> dp(n, 1);                 // 以item[i].second为末尾的最长增长子序列长度
    for (int i = 1; i < n; i++) {
      for (int j = 0; j < i; j++) {
        if (item[i].second > item[j].second) {  // 进行状态转移
          dp[i] = max(dp[i], dp[j] + 1);
        }
      }
    }
    int ans = *max_element(dp.begin(), dp.end());
    cout << ans << endl;
  }
}

超时，过不了，只能使用二分查找解法了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
using namespace std;

int main() {
  int T;
  cin >> T;
  for (int k = 0; k < T; k++) {
    int n, x, y;
    cin >> n;
    vector<pair<int, int>> item(n);
    for (int i = 0; i < n; i++) {
      cin >> item[i].first;
    }
    for (int i = 0; i < n; i++) {
      cin >> item[i].second;
    }
    auto cmp = [](const pair<int, int>& p1, const pair<int, int>& p2) -> bool { return p1.first < p2.first || (p1.first == p2.first && p1.second > p2.second); };
    sort(item.begin(), item.end(), cmp);  // 使用自定义排序函数
    int piles = 0;                        // 牌堆数
    for (int i = 0; i < n; i++) {
      int left = 0;
      int right = piles;
      int poker = item[i].second;  // 待放置的扑克牌
      while (left < right) {
        int mid = (left + right) / 2;
        if (item[mid].second >= poker) {
          right = mid;
        } else {
          left = mid + 1;
        }
      }
      if (left == piles) {  // 新建牌堆
        piles++;
      }
      item[left].second = poker;  // 放置牌堆顶
    }
    cout << piles << endl;
  }
}

第二题 小强爱数学


记忆深刻的问题，之前写过一遍，当时也是写了很久没写出来，看了一下午愣是没看出为啥答案错了

题目的难点在于想出这个递推公式，然后就是mod运算的性质，不过我出错的点在于使用int存储A，B，并用A，B计算了一次dp[2]，运算过程会溢出，即使dp[2]为long long，但表达式的组成元素类型全部为int，故仍然会发生溢出。

1
2
int A,B;
long long x = A * A - 2 * B;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using namespace std;
const int kMod = 1e9 + 7;
using ll = long long;
int main() {
  int T;
  cin >> T;
  for (int k = 0; k < T; k++) {
    ll A, B, n;  // 设置为long long，防止溢出
    cin >> A >> B >> n;
    vector<ll> dp(n + 3);
    dp[0] = 2;
    dp[1] = A;
    for (int i = 2; i <= n; i++) {  // fn = A * fn-1 - B * fn-2
      dp[i] = (dp[i - 1] * A % kMod - dp[i - 2] * B % kMod + kMod) % kMod;
    }
    cout << dp[n] << endl;
  }
}